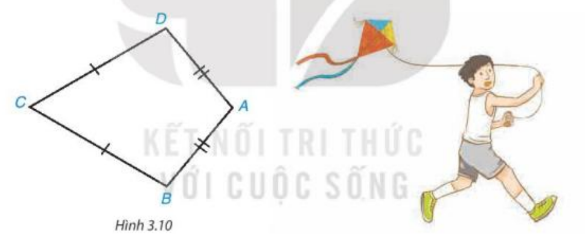
Giải SGK Toán 8 trang 51 Kết nối tri thức tập 1

Bài 3.1 trang 51 SGK Toán 8 tập 1 - Kết nối tri thức

Tính góc chưa biết của các tứ giác trong Hình 3.8.

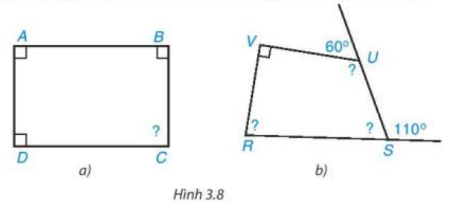
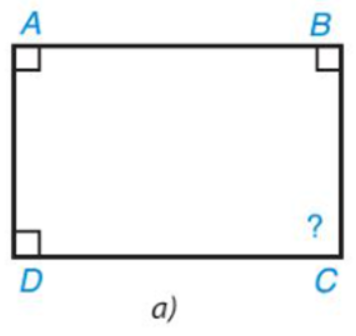
Lời giải:

• Hình 3.8a)

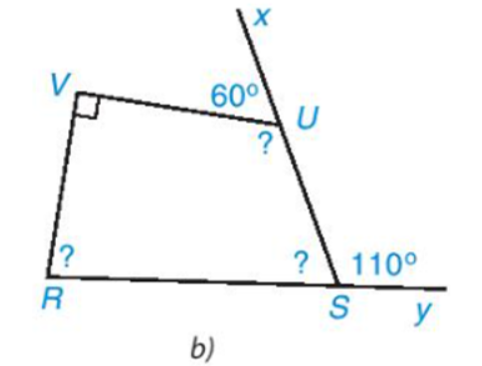
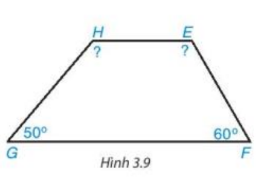
Xét tứ giác ABCD có: 

$\widehat A + \widehat B + \widehat C + \widehat D = {360^o}$

Hay 90°+90°+ˆC+90°=360°

Khi đó $\widehat C$+270°=360°

Do đó $\widehat C$=360°−270°=90°.

Vậy $\widehat C$=90°

• Hình 3.8b)

Vì $\widehat {{\rm{VUS}}}$ và $\widehat {VUx}$ là hai góc kề bù nên ta có: $\widehat {{\rm{VUS}}} + \widehat {VUx} = {180^o}$

Hay $\widehat {{\rm{VUS}}}$+60°=180°

Suy ra $\widehat {{\rm{VUS}}}$=180°−60°=120°

Vì $\widehat {US{\rm{R}}}$và $\widehat {USy}$là hai góc kề bù nên ta có: $\widehat {US{\rm{R}}} + \widehat {USy} = {180^o}$

Hay $\widehat {US{\rm{R}}}$+110°=180^o

Suy ra $\widehat {US{\rm{R}}}$ =180°−110°=70°

Do đó $\widehat {US{\rm{R}}}$=70°

Xét tứ giác VUSR có: 

$\widehat V + \widehat {{\rm{VUS}}} + \widehat {V{\rm{SR}}} + \widehat R = {360^o}$

Hay 90°+120°+70°+$\widehat R$=360°

Khi đó 280°+$\widehat R$=360°

Do đó $\widehat R$=360°−280°=80°

Vậy $\widehat R$=80° 

Bài 3.2 trang 51 SGK Toán 8 tập 1 - Kết nối tri thức

Tính góc chưa biết của tứ giác trong Hình 3.9. Biết rằng $\widehat H$=$\widehat E$+10^o

Lời giải:

Áp dụng định lí tổng bốn góc trong một tứ giác vào tứ giác HEFG, ta có:

$\widehat H + \widehat E + \widehat F + \widehat G = {360^o}$

$\widehat E$+10°+$\widehat E$+60°+50°=360^o

2$\widehat E$+120°=360°

Suy ra 2$\widehat E$=360°−120°=240°

Khi đó $\widehat E$=120°

Suy ra $\widehat H$=$\widehat E$+10°=120°+10°=130°

Vậy $\widehat H$=130°; $\widehat E$=120°

Bài 3.3 trang 51 SGK Toán 8 tập 1 - Kết nối tri thức

Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.

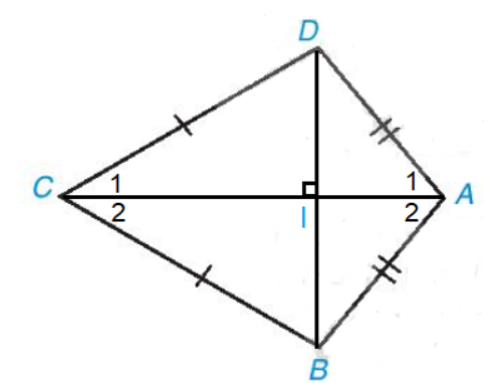
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.

b) Tính các góc B, D biết rằng $\widehat A$=100°,$\widehat C$=60°

Lời giải:

a) Nối AC, BD (như hình vẽ

Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;

CB = CD hay hai điểm C cách đều hai đầu mút B và D;

Do đó, hai điểm A và C cách đều hai đầu mút B và D.

Vậy AC là đường trung trực của đoạn thẳng BD.

b) Gọi I là giao điểm của AC và BD.

Vì AC là đường trung trực của đoạn thẳng BD nên AC ⊥ BD.

• Xét tam giác ABD cân tại A (vì AB = AD) có AI là đường cao (vì AI ⊥ BD)

Nên AI cũng là tia phân giác của $\widehat {BA{\rm{D}}}$ hay $\widehat {{A_1}} = \widehat {{A_2}}$

Suy ra $\widehat {{A_1}} = \widehat {{A_2}} = \widehat {B{\rm{D}}A}:2 = {100^o}:2 = {50^o}$

• Xét tam giác BCD cân tại C (vì BC = CD) có CI là đường cao (vì AC ⊥ BD)

Nên CI cũng là tia phân giác của $\widehat {BC{\rm{D}}}$ hay $\widehat {{C_1}} = \widehat {{C_2}}$

Suy ra $\widehat {{C_1}} = \widehat {{C_2}} = \widehat {BC{\rm{D}}}:2 = {60^o}:2 = {30^o}$

• Xét tam giác ACD có: $\widehat {{A_1}} + \widehat {{C_1}} + \widehat {A{\rm{D}}C} = {180^o}$ (định lí tổng ba góc trong một tam giác).

Hay 50°+30°+$\widehat {A{\rm{D}}C}$=180°

Suy ra $\widehat {A{\rm{D}}C}$=180°−50°−30°=100°

Xét tứ giác ABCD có:

$\widehat {BA{\rm{D}}} + \widehat {ABC} + \widehat {BC{\rm{D}}} + \widehat {A{\rm{D}}C} = {360^o}$(định lí tổng ba góc trong một tam giác).

Hay 100°+$\widehat {ABC}$+60°+100°=360°

Suy ra $\widehat {ABC}$+260°=360^o

Do đó $\widehat {ABC}$=360°−260°=100^o

Vậy $\widehat {ABC}$=100° ;$\widehat {A{\rm{D}}C}$=100° 

Sachbaitap.com