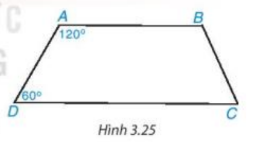
Giải SGK Toán 8 trang 56 Kết nối tri thức tập 1

Bài 3.9 trang 56 SGK Toán 8 tập 1 - Kết nối tri thức

Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?

Lời giải:

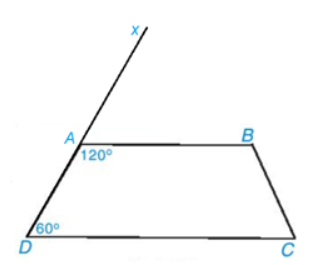
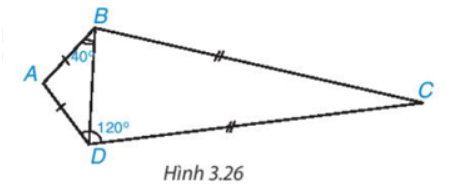
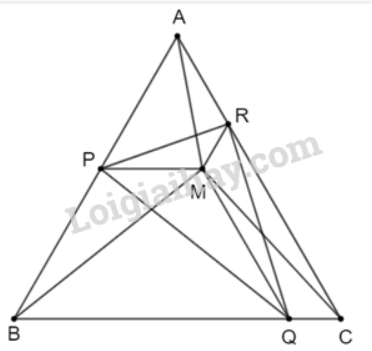
Vẽ tia Dx đi qua điểm A.

Vì \(\widehat {DAB}\) và \(\widehat {{\rm{BAx}}}\) là hai góc kề bù nên \(\widehat {DAB} + \widehat {{\rm{BAx}}} = {180^o}\)

Suy ra \(\widehat {{\rm{BAx}}} = {180^o} - \widehat {DAB} = {180^o} - {120^o} = {60^o}\)

Ta có \(\widehat {A{\rm{D}}C} = \widehat {{\rm{BAx}}} = {60^o}\)mà hai góc này ở vị trí đồng vị nên AB // CD.

Vậy tứ giác ABCD là hình thang.

Bài 3.10 trang 56 SGK Toán 8 tập 1 - Kết nối tri thức

Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết \(\widehat {AB{\rm{D}}} = {30^o}\), tính số đo các góc của hình thang đó.

Lời giải:

Xét tam giác ABD cân tại A (vì AB = AD), ta có:

• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {30^o}\)

• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\) hay \(\widehat A + {30^o} + {30^o} = {180^o}\)

Suy ra \(\widehat A\)=180°−30°−30°=120^o

Vì AB // CD nên \(\widehat {A{\rm{B}}D} = \widehat {B{\rm{D}}C} = {30^o}\) (hai góc so le trong).

Do đó \(\widehat {ADC} = \widehat {A{\rm{D}}B} + \widehat {C{\rm{D}}B}\)=30°+30°=60°

Vì tứ giác ABCD là hình thang cân nên \(\widehat {ADC} = \widehat C\)=60°

Ta có: \(\widehat A + \widehat {ABC} + \widehat C + \widehat {A{\rm{D}}C} = {360^o}\)

120°+60°+60°+\(\widehat {A{\rm{B}}C}\)=360°

240°+\(\widehat {A{\rm{B}}C}\)=360°

Suy ra =360°−240°=120°

Vậy số đo các góc của hình thang ABCD là \(\widehat A = {120^o};\widehat {ABC} = {120^o};\widehat {C} = {60^o};\widehat {A{\rm{D}}C} = {60^o}\).

Bài 3.11 trang 56 SGK Toán 8 tập 1 - Kết nối tri thức

Tính số đo các góc của tứ giác ABCD trong Hình 3.26.

Lời giải:

* Xét tam giác ABD cân tại A (vì AB = AD) ta có:

• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {40^o}\)

• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\)

Suy ra \(\widehat A\)=180°−\(\widehat {AB{\rm{D}}}\)−\(\widehat {A{\rm{D}}B}\)=180°−40°−40°=100°

Ta có \(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C}\)=120° suy ra \(\widehat {B{\rm{D}}C}\)=120°−\(\widehat {A{\rm{D}}B}\)=120°−40°=80°.

* Xét tam giác BCD cân tại C (vì BC = CD) ta có:

• \(\widehat {CB{\rm{D}}} = \widehat {C{\rm{D}}B}\)=80°

• \(\widehat C + \widehat {CB{\rm{D}}} + \widehat {C{\rm{D}}B}\)=180°

Suy ra \(\widehat C\)=180°−\(\widehat {CB{\rm{D}}} - \widehat {C{\rm{D}}B}\)=180°−80°−80°=20°

Ta có: \(\widehat {ABC} = \widehat {AB{\rm{D}}} + \widehat {CB{\rm{D}}}\)=40°+80°=120^o

Vậy số đo các góc của tứ giác ABCD là \(\widehat A = {100^o};\widehat {ABC} = {120^o};\widehat C = {20^o}\)

Bài 3.12 trang 56 SGK Toán 8 tập 1 - Kết nối tri thức

Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.

a) Chứng minh tứ giác APMR là hình thang cân

b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.

c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?

Lời giải:

a) Vì tam giác ABC đều nên \(\widehat {BAC} = \widehat {ABC} = \widehat {ACB} = {60^o}\)

Vì PM // BC nên \(\widehat {ABC} = \widehat {APM} = {60^o}\)

Tứ giác APMR là hình thang (vì MR // AP) có \(\widehat {ABC} = \widehat {APM}\)

Do đó tứ giác APMR là hình thang cân.

b) Vì tứ giác APMR là hình thang cân nên AM = PR        (1)

Vì MQ // AC nên \(\widehat {BQM} = \widehat {ACB} = {60^o}\)

Tứ giác BPMQ là hình thang (vì PM // BQ) có \(\widehat {BQM} = \widehat {ACB}\) nên BPMQ là hình thang cân.

Suy ra BM = PQ    (2)

Chứng minh tương tự, ta có MC = QR          (3)

Từ (1); (2) và (3) suy ra PR + BM + QR = MA + MB + MC.

Do đó chu vi tam giác PQR bằng tổng độ dài MA + MB + MC (đpcm).

c) Vì chu vi tam giác PQR bằng tổng độ dài MA + MB + MC

Để tam giác PQR là tam giác đều thì PQ = QR = PR suy ra MA = MB = MC

Khi đó điểm M cách đều ba đỉnh A, B, C của tam giác ABC.

Do đó M là giao điểm của ba đường trung trực (đồng thời M cũng là giao điểm của ba đường trung tuyến, ba đường cao, đường phân giác).

Vậy khi M là giao điểm của ba đường trung trực thì tam giác PQR là tam giác đều.

Sachbaitap.com