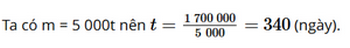Giải SGK Toán 8 trang 70 Cánh Diều tập 1

Bài 1 trang 70 SGK Toán 8 tập 1 - Cánh Diều

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước

b) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước và a khác 0.

c) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước và b khác 0.

Phương pháp:

Dựa vào định nghĩa hàm số bậc nhất

Lời giải:

a) Sai

b) Đúng

c) Sai

d) Đúng

Bài 2 trang 70 SGK Toán 8 tập 1 - Cánh Diều

Xác định hệ số của x, hệ số tự do trong mỗi hàm số bậc nhất sau:

\(a) y = 6{\rm{x}} + 8\)                         

\(b) y =  - x - 5\)                    

\(c) y = \dfrac{x}{3}\)

Phương pháp:

Hàm số y = ax + b \(\left( {a \ne 0} \right)\) có hệ số của x là a; hệ số tự do là b.

Lời giải:

a) Hàm số y = 6x + 8 có hệ số của x là 6; hệ số tự do là 8;

b) Hàm số y = – x – 5 có hệ số của x là 1; hệ số tự do là – 5;

Bài 3 trang 70 SGK Toán 8 tập 1 - Cánh Diều

Cho hàm số bậc nhất \(f(x) = 3{\rm{x}} + 2\). Tính \(f(1);f(0);f( - 2);f\left( {\dfrac{1}{2}} \right);f\left( { - \dfrac{2}{3}} \right)\).

Phương pháp:

Thay các giá trị \(x = 1;x = 0;x =  - 2;x = \frac{1}{2};x =  - \frac{2}{3}\) vào công thức \(f(x) = 3{\rm{x}} + 2\)

Lời giải:

Ta có:

\(\begin{array}{l}f(1) = 3.1 + 2 = 5;\\f(0) = 3.0 + 2 = 2\\f( - 2) = 3.\left( { - 2} \right) + 2 = 4;\\f\left( {\dfrac{1}{2}} \right) = 3.\dfrac{1}{2} + 2 = \dfrac{7}{2};\\f\left( { - \dfrac{2}{3}} \right) = 3.\left( { - \dfrac{2}{3}} \right) + 2 = 0\end{array}\)

Bài 4 trang 70 SGK Toán 8 tập 1 - Cánh Diều

Hiện tại, bạn Nam đã để dành được 300 000 đồng. Bạn Nam đang có ý định mua một chiếc xe đạp trị giá 2 000 000 đồng. Đẻ thực hiện được điều trên, bạn Nam đã lên kế hoạch hằng ngày đều tiết kiệm 5 000 đồng. Gọi m (đồng) là số tiền bạn Nam tiết kiệm được sau 1 ngày.

a) Viết công thức biểu thị m theo t. Hỏi m có phải là hàm số bậc nhất của t hay không?

b) Hỏi sau bao nhiêu ngày kể từ ngày bắt đầu tiết kiệm thì bạn Nam có thể mua được chiếc xe đạp đó?

Phương pháp:

- Mỗi ngày tiết kiệm được 5 000 đồng suy ra công thức tính số tiền tiết kiệm

- Tính số tiền phải tiết kiệm chia cho 5 000 sẽ ra số ngày cần phải tiết kiệm có thể mua được chiếc xe đạp

Lời giải:

a) Mỗi ngày bạn Nam tiết kiệm 5 000 đồng.

Với mỗi giá trị của t thì ta xác định được giá trị m tương ứng và  5 000 ≠ 0.

Do đó, m là hàm số bậc nhất của t.

b) Số tiền còn lại Nam cần để dành để Nam đủ tiền mua chiếc xe đạp là:

2 000 000 – 300 000 = 1 700 000 (đồng).

Khi đó, m = 1 700 000 (đồng).

Vậy sau 340 ngày kể từ ngày bắt đầu tiết kiệm thì bạn Nam có thể mua được chiếc xe đạp đó.

Bài 5 trang 70 SGK Toán 8 tập 1 - Cánh Diều

Một người đang sử dụng internet, mỗi phút tốn dung lượng 1 MB. Giả sử gói cước Internet của người đó cho phép sử dụng dung lượng 4 MB.

a) Viết hàm số f(x) biểu thị dung lượng tiêu tốn (MB) theo thời gian sử dụng internet x (giây).

b) Viết hàm số g(x) biểu thị dung lượng còn lại (MB) sau khi sử dụng Internet được x (giây).

c) Sau khi sử dụng Internet 2 phút thì dung lượng cho phép còn lại bao nhiêu Megabyte?

Phương pháp:

Dựa theo dữ kiệm mỗi phút tốn dung lượng 1 MB để biểu thị được dung lượng tiêu tốn MB sau khi sử dụng internet được x (giây)

Dung lượng còn lại bằng 4 trừ đi dung lượng đã sử dụng.

Lời giải:

c) Cách 1:

Mỗi phút tốn dung lượng 1 MB nên sau khi sử dụng Internet 2 phút thì tiêu tốn 2 MB.

Dung lượng còn lại cho phép còn lại là: 4 – 2 = 2 (MB).

Vậy sau khi sử dụng Internet 2 phút thì dung lượng còn lại cho phép còn lại là 2 Megabyte.

Bài 6 trang 70 SGK Toán 8 tập 1 - Cánh Diều

Bạn Dương mang theo 100 000 đồng và đạp xe đạp đi nhà sách để mua vở. Biết giá mỗi quyển vở là  7 000 đồng, phí gửi xe đạp là 3000 đồng.

a) Viết công thức biểu thị tổng số tiền y (đồng) bạn Dương cần phải trả cho việc gửi xe đạp và mua x quyển vở. Hỏi y có phải là hầm số bậc nhất của x hay không?

b) Tính số tiền bạn Dương phải trả khi gửi xe và mua 12 quyển vở?

c) Viết công thức biểu thị số tiền còn lại t (đồng) bạn Dương còn lại sau khi gửi xe và mua x quyển vở. Hàm số cho bởi công thức đó có phải là hàm số bậc nhất hay không?

d) Với số tiền trên, bạn Dương có thể mua được 15 quyển vở hay không? Vì sao?

Phương pháp:

Dựa vào dữ kiện đề bài đưa ra để viết các công thức theo yêu cầu.

Lời giải:

a) Công thức biểu thị tổng số tiền y (đồng) bạn Dương cần phải trả cho việc gửi xe đạp và mua x quyển vở là: y = 7000.x+ 3 000 (đồng)

y là hàm số bậc nhất của x

b) Số tiền bạn Dương phải trả khi gửi xe và mua 12 quyển vở là: y = 7000. 12+ 3 000 = 87 000 (đồng)

c) Công thức biểu thị số tiền còn lại t (đồng) bạn Dương còn lại sau khi gửi xe và mua x quyển vở là:

t = 100 000 – (7000.x + 3 000) = -7000.x + 97 000 (đồng)

t là hàm số bậc nhất của x

d) Với số tiền trên, bạn Dương không thể mua được 15 quyển vở vì mua 15 quyển vở hết:

7000. 15 = 105 000 (đồng) mà bạn Dương có 100 000 nên không đủ.

Sachbaitap.com