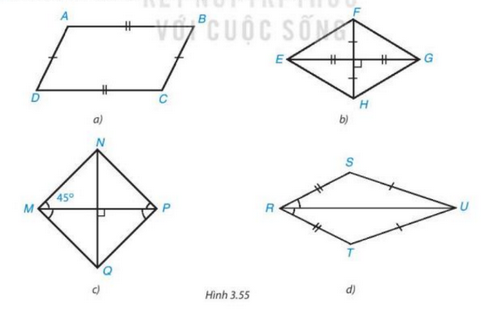
Giải SGK Toán 8 trang 71, 72 Kết nối tri thức tập 1

Bài 3.29 trang 71 SGK Toán 8 tập 1 - Kết nối tri thức

Tìm hình thoi và hình vuông trong Hình 3.55.

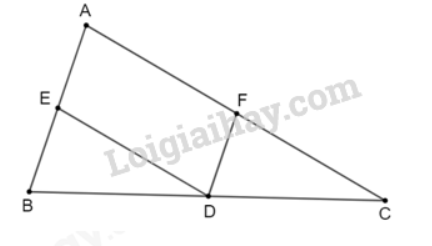
Lời giải:

* Xét Hình 3.55a)

Tứ giác ABCD có AB = CD; AD = BC.

Suy ra tứ giác ABCD là hình bình hành.

* Xét Hình 3.55b)

Tứ giác EFGH có hai đường chéo EG và FH cắt nhau tại trung điểm của mỗi đường.

Suy ra tứ giác EFGH là hình bình hành.

Hình bình hành EFGH có hai đường chéo vuông góc với nhau

Do đó tứ giác EFGH là hình thoi.

Bài 3.30 trang 72 SGK Toán 8 tập 1 - Kết nối tri thức

Cho tam giác ABC, D là một điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB, AC, chúng cắt các cạnh AC, AB lần lượt tại E, F.

a) Tứ giác AEDF là hình gì? Vì sao?

b) Nếu tam giác ABC cân tại A thì điểm D ở vị trí nào trên cạnh BC để tứ giác AEDF là hình thoi?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì?

d) Nếu tam giác ABC vuông cân tại A thì điểm D ở vị trí nào trên cạnh BC để AEDF là hình vuông?

Lời giải:

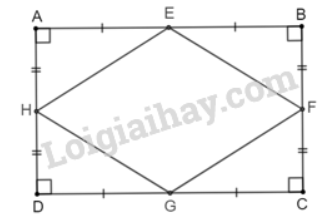
a) Tứ giác AEDF có AE // DF; AF // DE (giả thiết).

Suy ra tứ giác AEDF là hình bình hành.

b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A.

Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.

c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì hình vuông là hình bình hành có một góc vuông).

d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì hình vuông vừa là hình chữ nhật, vừa là hình thoi).

Bài 3.31 trang 72 SGK Toán 8 tập 1 - Kết nối tri thức

Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.

Lời giải:

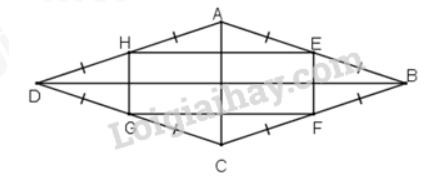
Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD.

Suy ra EH là đường trung bình của tam giác ABD.

Do đó \(EH = \frac{{E{\rm{D}}}}{2}\)         (1)

Chứng minh tương tự, ta có: \(FG = \frac{{B{\rm{D}}}}{2}{\rm{;EF = }}\frac{{AC}}{2};HG = \frac{{AC}}{2}\)    (2)

Lại có, ABCD là hình chữ nhật nên AC = BD         (3)

Từ (1), (2) và (3) suy ra EF = FG = GH = HE.

Do đó tứ giác ABCD là hình thoi.

Bài 3.32 trang 72 SGK Toán 8 tập 1 - Kết nối tri thức

Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.

Lời giải:

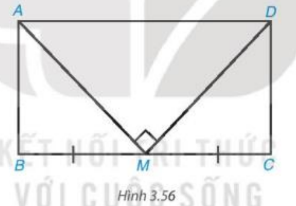
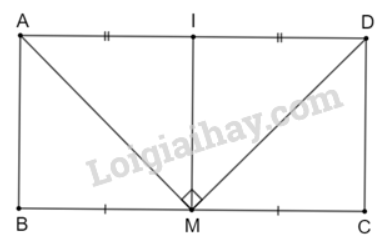
Xét tam giác ABC có E và F lần lượt là trung điểm của AB và BC.

Suy ra EF là đường trung bình của tam giác ABC.

Do đó EF // AC và \[{\rm{EF}} = \frac{{AC}}{2}\]    (1)

* Tương tự tam giác ADC có HG là đường trung bình nên:

HG // AC và \(HG = \frac{{AC}}{2}\)  (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG.

Suy ra tứ giác EFGH là hình bình hành.

Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF.

EH // BD và EF ⊥ BD nên EF ⊥ EH.

Nên \(\widehat {F{\rm{E}}H} = {90^o}\)

Hình bình hành EFGH có \(\widehat E = {90^o}\) nên là hình chữ nhật.

Bài 3.33 trang 72 SGK Toán 8 tập 1 - Kết nối tri thức

Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC. Biết rằng MA ⊥ MD. Tính độ dài các cạnh của hình chữ nhật ABCD (H.3.56).

Lời giải:

Gọi I là trung điểm của AD.

Khi đó, \(MI = \frac{{A{\rm{D}}}}{2}\) mà M là trung điểm của BC nên MI = AB.

Suy ra \(AB = \frac{{A{\rm{D}}}}{2}\) nên AD = 2AB.

Mà \(AB + A{\rm{D}} = \frac{{36}}{2} = 18\) (cm).

Suy ra AB + 2AB = 18

Hay 3AB = 18

Do đó AB = 6 (cm).

Suy ra AD = 2AB = 2 . 6 = 12 (cm).

Vậy độ dài các cạnh của hình chữ nhật ABCD là AB = CD = 6 cm; AD = BC = 12 cm.

Sachbaitap.com