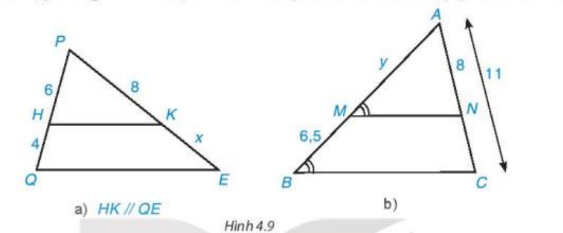
Giải SGK Toán 8 trang 80 Kết nối tri thức tập 1

Bài 4.1 trang 80 SGK Toán 8 tập 1 - Kết nối tri thức

Tìm độ dài x, y trong Hình 4.9 (làm tròn kết quả đến chữ số thập phân thứ nhất).

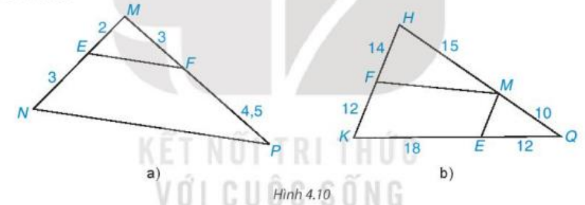
Lời giải:

• Hình 4.9a)

Vì HK // QE nên áp dụng định lí Thalès, ta có:

 \(\dfrac{{PH}}{{QH}} = \dfrac{{PK}}{{KE}}\)hay \(\dfrac{6}{4} = \dfrac{8}{x}\)

Suy ra \(x = \dfrac{{8.4}}{6} = \dfrac{{16}}{3} \approx 5,3\) (đvđd).

• Hình 4.9b)

Vì \(\widehat {AMN} = \widehat {ABC};\widehat {AMN}\) và \(\widehat {ABC}\) là hai góc đồng vị nên MN // BC.

Ta có AB = AM + BM = y + 6,5.

Áp dụng định lí Thalès, ta có: \(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}}\) hay \(\dfrac{y}{{y + 6,5}} = \dfrac{8}{{11}}\)

Suy ra 11y = 8(y + 6,5)

11y = 8y + 52

11y – 8y = 52

3y = 52

\(y = \dfrac{{52}}{3} \approx 17,3\) (đvđd)

Vậy x ≈ 5,3 (đvđd); y ≈ 17,3 (đvđd).

Bài 4.2 trang 80 SGK Toán 8 tập 1 - Kết nối tri thức

Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích tại sao chúng song song với nhau.

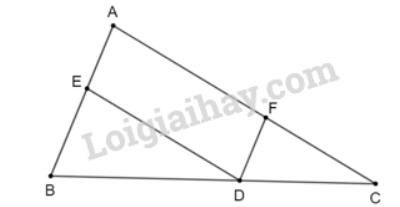
Lời giải:

• Hình 4.10a)

Ta có: \(\dfrac{{EM}}{{EN}} = \dfrac{2}{3};\dfrac{{MF}}{{PF}} = \dfrac{3}{{4,5}} = \dfrac{2}{3}\) nên \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\)

Vì \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\), E ∈ MN, F ∈ MP nên theo định lí Thalès đảo ta suy ra EF // MN.

• Hình 4.10b)

* Ta có: \(\dfrac{{HF}}{{KF}} = \dfrac{{14}}{{12}} = \dfrac{7}{6};\dfrac{{HM}}{{MQ}} = \dfrac{{15}}{{10}} = \dfrac{3}{2}\)

Vì \(\dfrac{{HF}}{{KF}} \ne \dfrac{{HM}}{{MQ}}\) nên MF không song song với KQ.

* Ta có: \(\dfrac{{MQ}}{{MH}} = \dfrac{{10}}{{15}} = \dfrac{2}{3};\dfrac{{EQ}}{{EK}} = \dfrac{{12}}{{18}} = \dfrac{2}{3}\)

Vì \(\dfrac{{MQ}}{{MH}} = \dfrac{{EQ}}{{EK}}\); F ∈ HK; M ∈ HQ nên theo định lí Thalès đảo ta suy ra ME // HK.

Bài 4.3 trang 80 SGK Toán 8 tập 1 - Kết nối tri thức

Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E.

Chứng minh rằng: \(\dfrac{{A{\rm{E}}}}{{AB}} + \dfrac{{AF}}{{AC}} = 1\)

Lời giải:

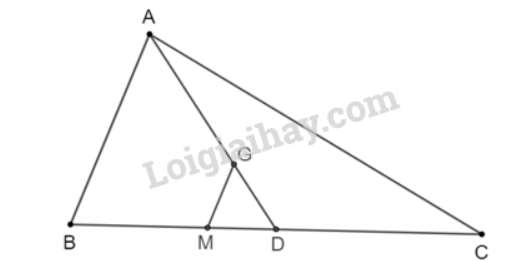
Áp dụng định lí Thalès, ta có:

• Vì DE // AC nên \(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{C{\rm{D}}}}{{BC}}\)

• Vì DF // AC nên \(\dfrac{{AF}}{{AC}} = \dfrac{{B{\rm{D}}}}{{BC}}\)

Khi đó, \(\dfrac{{A{\rm{E}}}}{{AB}} + \dfrac{{AF}}{{AC}} = \dfrac{{C{\rm{D}}}}{{BC}} + \dfrac{{B{\rm{D}}}}{{BC}} = 1\) (đpcm).

Bài 4.4 trang 80 SGK Toán 8 tập 1 - Kết nối tri thức

Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng \(BM = \dfrac{1}{3}BC\)

Lời giải:

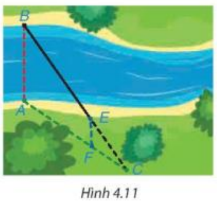
Lấy D là trung điểm của cạnh BC.

Khi đó, AD là đường trung tuyến của tam giác ABC.

Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.

Ta có \(\dfrac{{AG}}{{A{\rm{D}}}} = \dfrac{2}{3}\) hay \(AG = \dfrac{2}{3}A{\rm{D}}\)

Vì MG // AB, theo định lí Thalès, ta suy ra: \(\dfrac{{AG}}{{A{\rm{D}}}} = \dfrac{{BM}}{{B{\rm{D}}}} = \dfrac{2}{3}\)

Ta có BD = CD (vì D là trung điểm của cạnh BC) nên \(\dfrac{{BM}}{{BC}} = \dfrac{{BM}}{{2B{\rm{D}}}} = \dfrac{2}{{2.3}} = \dfrac{1}{3}\)

Do đó \(BM = \dfrac{1}{3}BC\) (đpcm).

Bài 4.5 trang 80 SGK Toán 8 tập 1 - Kết nối tri thức

Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF (H.4.11). Sau đó bác An đo được AF = 40 m, FC = 20 m, EC = 30 m. Hỏi khoảng cách giữa hai vị trí B và E bằng bao nhiêu?

Lời giải:

Theo đề bài, ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF, áp dụng định lí Thalès, ta có:

\(\dfrac{{EC}}{{BE}} = \dfrac{{CF}}{{AF}}\) hay \(\dfrac{{30}}{{BE}} = \dfrac{{20}}{{40}}\)

Suy ra \(BE = \dfrac{{30.40}}{{20}} = 60\) (m).

Vậy khoảng cách giữa hai vị trí B và E bằng 60 m.

Sachbaitap.com