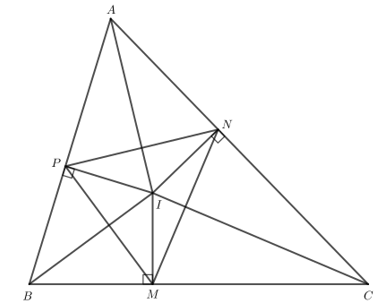
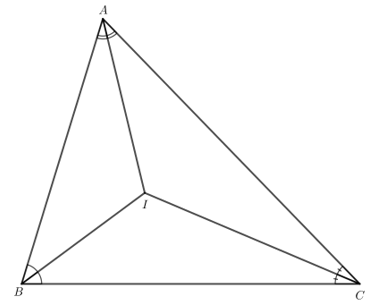
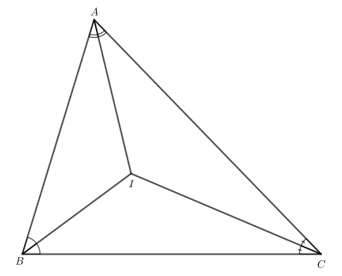
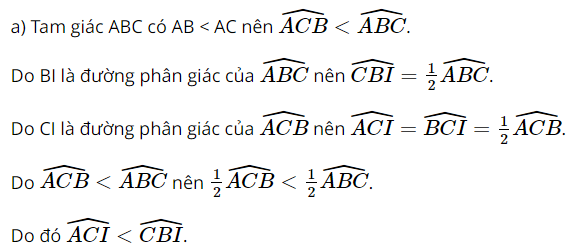Giải Toán 7 trang 111 Cánh Diều tập 2

Bài 1 trang 111 SGK Toán 7 tập 2 - Cánh Diều

Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.

a) Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao?

b) Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?

Phương pháp:

a) Dựa vào tính chất của ba đường phân giác trong tam giác: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác.

b) Dựa vào chứng minh các cặp tam giác bằng nhau.

Lời giải:

a) Tam giác ABC có I là giao điểm ba đường phân giác nên I cách đều 3 cạnh của tam giác ABC.

Do đó IM = IN = IP.

Do IM = IN nên tam giác IMN cân tại I.

Do IN = IP nên tam giác INP cân tại I.

Do IP = IM nên tam giác IPM cân tại I.

b) Xét ∆AIP vuông tại P và ∆AIN vuông tại N có:

AI chung.

IP = IN (theo giả thiết).

Do đó ∆AIP = ∆AIN (cạnh huyền - cạnh góc vuông).

Suy ra AP = AN (2 cạnh tương ứng).

Tam giác ANP có AP = AN nên tam giác ANP cân tại A.

Xét ∆BIP vuông tại P và BIM vuông tại M có:

BI chung.

IP = IM (theo giả thiết).

Do đó ∆BIP = ∆BIM (cạnh huyền - cạnh góc vuông).

Suy ra BP = BM (2 cạnh tương ứng).

Tam giác BPM có BP = BM nên tam giác BPM cân tại B.

Xét ∆CIM vuông tại M và ∆CIN vuông tại N có:

CI chung.

IM = IN (theo giả thiết).

Do đó ∆CIM = ∆CIN (cạnh huyền - cạnh góc vuông).

Suy ra CM = CN (2 cạnh tương ứng).

Tam giác CMN có CM = CN nên tam giác CMN cân tại C.

Bài 2 trang 111 SGK Toán 7 tập 2 - Cánh Diều

Tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh:

a) \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \);                                       

b) \(\widehat {BIC} = 90^\circ  + \dfrac{1}{2}\widehat {BAC}\).

Phương pháp:

a) Dựa vào tính chất của đường phân giác: chia các góc tại các đỉnh thành hai góc bằng nhau.

b) Dựa vào kết quả của phần a).

Lời giải:

Bài 3 trang 111 SGK Toán 7 tập 2 - Cánh Diều

Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.

a) Chứng minh \(\widehat {CBI} > \widehat {ACI}\);                                            

b) So sánh IB và IC.

Phương pháp:

a) Góc đối diện với cạnh lớn hơn thì có số đo góc lớn hơn.

b) Cạnh đối diện với góc lớn hơn thì có số đo độ dài lớn hơn.

Lời giải:

Sachbaitap.com