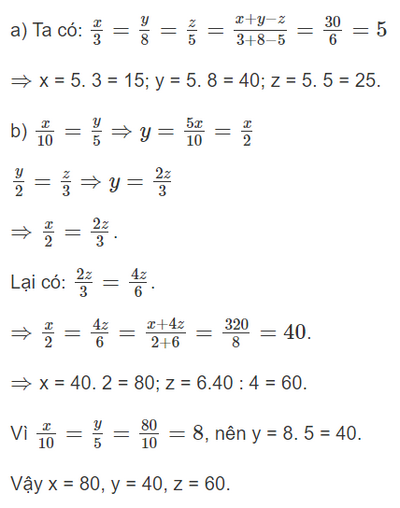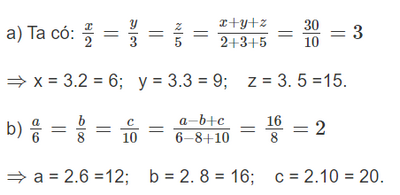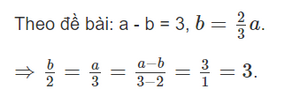Giải Toán 7 trang 23 Chân trời sáng tạo tập 2

Bài 1 trang 23 SGK Toán 7 tập 2 - Chân trời sáng tạo

Tìm x,y,z biết:

a) \(\dfrac{x}{3} = \dfrac{y}{8} = \dfrac{z}{5}\) và x + y – z = 30

b) \(\dfrac{x}{{10}} = \dfrac{y}{5}\);\(\dfrac{y}{2} = \dfrac{z}{3}\) và x + 4z = 320

Phương pháp:

Sử dụng tính chất của dãy tỉ số bằng nhau: \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{x \pm y \pm z}}{{a \pm b \pm c}}\)

Lời giải:

Bài 2 trang 23 SGK Toán 7 tập 2 - Chân trời sáng tạo

Hai bạn Mai và Hoa đi xe đạp từ trường đến nhà thi đấu để học bơi. Vận tốc của Mai kém vận tốc của Hoa là 3 km/h. Thời gian Mai và Hoa đi từ trường đến nhà thi đấu lần lượt là 30 phút, \(\dfrac{2}{5}\) giờ. Hỏi quãng đường từ trường đến nhà thi đấu dài bao nhiêu kilômét?

Phương pháp:

Vận tốc và thời gian đi cùng một quãng đường là hai đại lượng tỉ lệ nghịch

Lời giải:

Gọi x và y lần lượt là vận tốc của Mai và Hoa đi xe đạp. (x> 3; y > 0).

Theo đề bài ta có: y - x = 3.

⇒ x = 6. 2 = 12.

Vậy quãng đường từ trường đến nhà thì đấu dài: 12. 0,5 = 6 (km).

Bài 3 trang 23 SGK Toán 7 tập 2 - Chân trời sáng tạo

Số quyển sách của ba bạn An, Bình và Cam tỉ lệ với các số 3; 4; 5. Hỏi mỗi bạn có bao nhiêu quyển sách? Biết rằng số quyển sách của Bình ít hơn tổng số quyển sách của An và Cam là 8 quyển sách.

Phương pháp:

Áp dụng tính chất của dãy tỉ số bằng nhau \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{x \pm y \pm z}}{{a \pm b \pm c}}\)

Lời giải:

Bài 4 trang 23 SGK Toán 7 tập 2 - Chân trời sáng tạo

a) Tìm ba số x,y,z thỏa mãn x : y : z = 2 : 3 : 5 và x + y + z = 30     

b) Tìm ba số a,b,c thỏa mãn a : b : c = 6 : 8 : 10 và a – b + c = 16

Phương pháp:

Áp dụng tính chất của dãy tỉ số bằng nhau \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{x \pm y \pm z}}{{a \pm b \pm c}}\)

Lời giải:

Bài 5 trang 23 SGK Toán 7 tập 2 - Chân trời sáng tạo

Tổng số học sinh của hai lớp 7A và 7B là 55 học sinh. Tìm số học sinh của mỗi lớp biết rằng số học sinh lớp 7A bằng \(\dfrac{5}{6}\) số học sinh lớp 7B.

Phương pháp:

Ta lập tỉ số giữa học sinh của 2 lớp rồi áp dụng tính chất của dãy tỉ số bằng nhau.

Sau đó tính được số học sinh của mỗi lớp

Lời giải:

Bài 6 trang 23 SGK Toán 7 tập 2 - Chân trời sáng tạo

Linh và Nam thi nhau giải toán ôn tập cuối học kì. Kết quả là Linh làm được nhiều hơn Nam 3 bài và số bài Nam làm được chỉ bằng \(\dfrac{2}{3}\)số bài của Linh làm được. Hãy tìm số bài mỗi bạn làm được.

Phương pháp:

Áp dụng tính chất của dãy tỉ số bằng nhau :\(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a - c}}{{b - d}}\)

Lời giải:

Gọi số bài Linh và Nam làm được lần lượt là: a, b. (a,b∈N;a,b>0).

⇒ a = 9; b = 6.

Vậy số bài bạn Linh và Nam làm được lần lượt là: 9 và 6 bài.

Bài 7 trang 23 SGK Toán 7 tập 2 - Chân trời sáng tạo

Lớp 7A có 4 bạn làm vệ sinh xong lớp học hết 2 giờ. Hỏi nếu có 16 bạn sẽ làm vệ sinh xong lớp học trong bao lâu? (Biết rằng các bạn có năng suất làm việc như nhau)

Phương pháp:

Thời gian và số bạn làm là hai đại lượng tỉ lệ nghịch.

Áp dụng tính chất 2 đại lượng tỉ lệ nghịch.

Lời giải:

Do thời gian làm vệ sinh và số học sinh là hai đại lượng tỉ lệ nghịch với nhau, nên ta có: 4. 2 = 16. t

⇒ t = 4. 2 : 16 = 0,5.

Vậy nếu 16 bạn sẽ làm vệ sinh xong lớp học trong 0,5 giờ (hay 30 phút).

Bài 8 trang 23 SGK Toán 7 tập 2 - Chân trời sáng tạo

Bạn Hà muốn chia đều 1 kg đường vào n túi. Gọi p (g) là lượng đường trong mỗi túi. Hãy chứng tỏ n,p là hai đại lượng tỉ lệ nghịch và tính p theo n

Phương pháp:

Chứng minh p.n = a không đổi với a ≠ 0

Lời giải:

Chia 1 kg = 1000 g đường vào n túi, mỗi túi p (g) nên ta có: n.p = 1000, nên n và p là hai đại lượng tỉ lệ nghịch với nhau.

Bài 9 trang 23 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho biết mỗi lít dầu ăn có khối lượng 0,8 kg.

a) Giả sử x lít dầu ăn có khối lượng y kg. Hãy viết công thức tính y theo x.

b) Tính thể tích của 240g dầu ăn.

Phương pháp:

+) Nếu hai đại lượng y và x liên hệ với nhau theo công thức y = k .x ( k khác 0, không đổi) thì y và x là hai đại lượng tỉ lệ thuận.

+) Áp dụng tính chất hai đại lượng tỉ lệ thuận.

Lời giải:

a) Mỗi lít dầu ăn có khối lượng 0,8 kg, suy ra x lít dầu ăn có khối lượng y = 0,8.x.

b) 240 g = 0,24 kg.

Thể tích của 240 gam dầu ăn là: 0,24 : 0,8 = 0,3 lít.

Sachbaitap.com