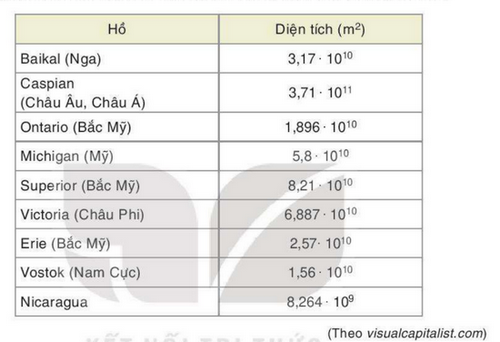
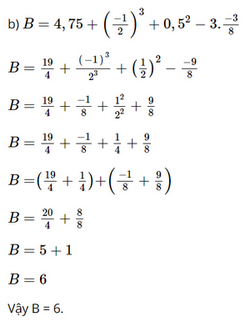Giải Toán 7 trang 24 Kết nối tri thức với cuộc sống tập 1

Bài 1.31 trang 22 SGK Toán 7 tập 1 - Kết nối tri thức

Tìm x, biết:

\(\begin{array}{l}a)2x + \frac{1}{2} = \frac{7}{9}\\b)\frac{3}{4} - 6x = \frac{7}{{13}}\end{array}\)

Phương pháp:

Chuyển vế, tìm x

Lời giải:

\(\begin{array}{l}a)2x + \frac{1}{2} = \frac{7}{9}\\2x = \frac{7}{9} - \frac{1}{2}\\2x = \frac{{14}}{{18}} - \frac{9}{{18}}\\2x = \frac{5}{{18}}\\x = \frac{5}{{18}}:2\\x = \frac{5}{{18}}.\frac{1}{2}\\x = \frac{5}{{36}}\end{array}\)

Vậy \(x = \frac{5}{{36}}\)

\(\begin{array}{l}b)\frac{3}{4} - 6x = \frac{7}{{13}}\\ 6x = \frac{3}{{4}} - \frac{7}{13}\\ 6x = \frac{{39}}{{52}} - \frac{{28}}{{52}}\\ 6x = \frac{{11}}{{52}}\\x = \frac{{11}}{{52}}:6\\x = \frac{{11}}{{52}}.\frac{{1}}{6}\\x = \frac{{11}}{{312}}\end{array}\)

Vậy \(x = \frac{{11}}{{312}}\)

Bài 1.32 trang 22 SGK Toán 7 tập 1 - Kết nối tri thức

Diện tích một số hồ nước ngọt lớn nhất trên thế giới được cho trong bảng sau. Em hãy sắp xếp chúng theo thứ tự diện tích từ nhỏ đến lớn.

Phương pháp:

Đưa các số liệu về dạng \(a{.10^{10}}\) rồi so sánh.

Sắp xếp tên các hồ nước ngọt theo thứ tự diện tích từ nhỏ đến lớn

Lời giải:

Đổi 8,264.10⁹ = 0,8264.10.10⁹ = 0,8264.10¹⁰;    3,71.10¹¹ = 3,71.10.10¹⁰ = 37,1.10¹⁰.

Do 0,8264 < 1,56 < 1,896 < 2,57 < 3,17 < 5,8 < 6,887 < 8,21 < 37,1 nên

0,8264.10¹⁰ < 1,56.10¹⁰ < 1,896.10¹⁰ < 2,57.10¹⁰ < 3,17.10¹⁰ < 5,8.10¹⁰ < 6,887.10¹⁰

< 8,21 .10¹⁰ < 37,1.10¹⁰.

Hay 8,264.10⁹ < 1,56.10¹⁰ < 1,896.10¹⁰ < 2,57.10¹⁰ < 3,17.10¹⁰ < 5,8.10¹⁰ < 6,887.10¹⁰

< 8,21.10¹⁰ < 3,71.10¹¹.

Vậy tên các hồ nước ngọt theo thứ tự diện tích từ nhỏ đến lớn là: Nicaragua, Vostok, Ontario, Erie, Baikal, Michigan, Victoria, Superior, Caspian.

Bài 1.33 trang 22 SGK Toán 7 tập 1 - Kết nối tri thức

Tính một cách hợp lí:

\(\begin{array}{l}a)A = 32,125 - (6,325 + 12,125) - (37 + 13,675)\\b)B = 4,75 + {\left( {\frac{{ - 1}}{2}} \right)^3} + 0,{5^2} - 3.\frac{{ - 3}}{8}\\c)C = 2021,2345.2020,1234 + 2021,2345.( - 2020,1234)\end{array}\)

Phương pháp:

a) Phá ngoặc, nhóm các số hạng có tổng “đẹp”

b) Nhóm các số hạng là phân số có cùng mẫu số

c) Sử dụng tính phân phối của phép nhân đối với phép cộng: a.b + a.c = a.(b+c)

Lời giải:

a) A = 32,125 – (6,325 + 12,125) – (37 + 13,675)

A = 32,125 – 6,325 – 12,125 – 37 – 13,675

A = (32,125 – 12,125) – (6,325 + 13,675) – 37

A = 20 – 20 – 37

A = –37

Vậy A = –37.

c) C = 2021,2345 . 2020,1234 + 2021,2345 . (–2020,1234)

C = 2021,2345 . [2020,1234 + (–2020,1234)]

C = 2021,2345 . 0

C = 0

Vậy C = 0.

Bài 1.34 trang 22 SGK Toán 7 tập 1 - Kết nối tri thức

Đặt một cặp dấu ngoặc “( )” vào biểu thức sau để được kết quả bằng 0.

2,2 – 3,3 + 4,4 – 5,5.

Phương pháp:

Nhận thấy biểu thức đã cho chỉ gồm phép cộng và trừ, kết quả chưa bằng 0. Ta cần đặt dấu ngoặc trước dấu “-“ mới có thể thay đổi kết quả của biểu thức.

Lời giải:

Ta đặt dấu ngoặc vào biểu thức như sau:

2,2 – (3,3 + 4,4 – 5,5)

Khi đó giá trị của biểu thức là:

2,2 – (3,3 + 4,4 – 5,5)

= 2,2 – (7,7 – 5,5)

= 2,2 – 2,2

= 0. (thỏa mãn yêu cầu đề bài)

Sachbaitap.com