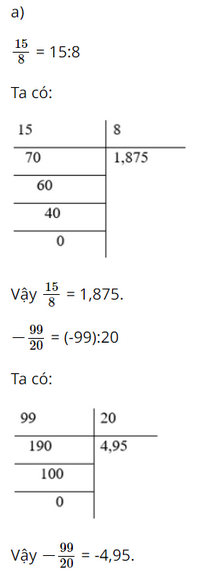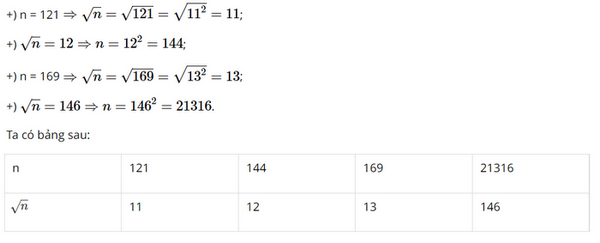Giải Toán 7 trang 33, 34 Chân trời sáng tạo tập 1Giải bài 1, 2, 3, 4 trang 33, bài 5, 6, 7, 8 trang 34 SGK Toán lớp 7 chân trời sáng tạo tập 1. Bài 8. Tìm số hữu tỉ trong các số sau: Bài 1 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo a) Hãy biểu diễn các số hữu tỉ sau đây dưới dạng số thập phân: \(\frac{{15}}{8};\,\,\,\frac{{ - 99}}{{20}};\,\,\,\frac{{40}}{9};\,\,\, - \frac{{44}}{7}\) b) Trong các số thập phân vừa tính được, hãy chỉ ra các số thập phân vô hạn tuần hoàn. Phương pháp: a)Thực hiện phép chia tử cho mẫu số để viết các số đã cho dưới dạng số thập phân. b) Các số thập phân vô hạn mà ở phần thập phân không có một chu kì nào cả. Lời giải:
b) Trong các số thập phân vừa tính được, các số thập phân vô hạn tuần hoàn là: 4,444…. = 4 (4) −6,285714285...">−6,285714285...−6,285714285...= -6,(285714) Bài 2 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo Chọn phát biểu đúng trong các phát biểu sau: \(a)\sqrt 2 \in I;\,\,\,\,\,b)\sqrt 9 \in I;\,\,\,\,c)\,\pi \in I;\,\,\,\,\,d)\sqrt 4 \in \mathbb{Q}\) Phương pháp: I là kí hiệu tập hợp các số vô tỉ Q là kí hiệu tập hợp các số hữu tỉ Lời giải:
Bài 3 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo Tính: \(a)\sqrt {64} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b)\sqrt {{{25}^2}} ;\,\,\,\,\,\,\,\,\,\,\,c)\sqrt {{{\left( { - 5} \right)}^2}} .\) Phương pháp: \(\sqrt {{a^2}} = \sqrt {{{\left( { - a} \right)}^2}} = a\) Lời giải: \(a)\sqrt {64} \, = \sqrt {{8^2}} = 8\,\,\,\,\,\,b)\sqrt {{{25}^2}} = 25;\,\,\,\,\,\,c)\sqrt {{{\left( { - 5} \right)}^2}} = 5\). Bài 4 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo Hãy thay dấu ? bằng các số thích hợp. Phương pháp: \(\sqrt {{a^2}} = a\) Lời giải:
Bài 5 trang 34 SGK Toán 7 tập 1 - Chân trời sáng tạo Dùng máy tính cầm tay để tính các căn bậc hai số học sau (làm tròn đến 3 chữ số thập phân). \(a)\sqrt {2250} ;\,\,\,\,\,\,b)\sqrt {12} ;\,\,\,\,\,\,\,c)\sqrt 5 \,\,\,\,\,\,\,\,\,d)\sqrt {624} \) Phương pháp: Dùng máy tính cầm tay để tính các căn bậc hai. Lời giải: \(a)\sqrt {2250} \approx 47,434;\,\,\,\,\,\,b)\sqrt {12} \approx 3,461;\,\,\,\,\,\,\,c)\sqrt 5 \approx 2,236\,\,\,\,\,\,\,\,\,d)\sqrt {624} \approx 24,980\) Bài 6 trang 34 SGK Toán 7 tập 1 - Chân trời sáng tạo Bác Thu thuê thợ lát gạch một cái sân hình vuông hết tất cả là 10 125 000 đồng. Cho biết chi phí cho 1 m2 (kể cả công thợ và vật liệu) là 125 000 đồng. Hãy tính chiều dài cạnh của cái sân. Phương pháp: -Diện tích của sân = gia tiền thuê lát sân : chi phí lát 1 m2 -Chiều dài của sân bằng căn bậc hai số học của diện tích sân. Lời giải: Diện tích cái sân là: 10 125 000 : 125 000 = 81 Vì cái sân có hình vuông nên chiều dài cái sân là: 81=9">√81 = 9 (m) Vậy chiều dài cái sân là 9m. Bài 7 trang 34 SGK Toán 7 tập 1 - Chân trời sáng tạo Tính bán kính của một hình tròn có diện tích là 9869 m2 (dùng máy tính cầm tay). Phương pháp: Áp dụng công thức: \(S = \pi .{R^2} \Rightarrow R = \sqrt {\frac{S}{\pi }} \) Lời giải:
Bài 8 trang 34 SGK Toán 7 tập 1 - Chân trời sáng tạo Tìm số hữu tỉ trong các số sau: \(12;\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{2}{3};\,\,\,\,\,\,3,\left( {14} \right);\,\,\,\,\,\,\,0,123;\,\,\,\,\,\,\,\,\sqrt 3 \) Phương pháp: Số hữu tỉ gồm các số thập phân hữu hạn và vô hạn tuần hoàn. Số vô tỉ gồm các số thập phân vô hạn không tuần hoàn. Lời giải: Ta có:
3,(14) là số hữu tỉ vì đây là số thập phân vô hạn tuần hoàn. 0,123 là số hữu tỉ vì đây là số thập phân hữu hạn.
Vậy các số hữu tỉ là: 12; 23; 3,14; 0,123">12; Sachbaitap.com
Xem thêm tại đây:
Bài 1. Số vô tỉ. Căn bậc hai số học - CTST
|
-

Giải Toán 7 trang 38 Chân trời sáng tạo tập 1
Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 38 SGK Toán lớp 7 chân trời sáng tạo tập 1. Bài 1. Hãy thay mỗi ? bằng kí hiệu ( in ) hoặc ( notin ) để có phát biểu đúng.

 Tải ngay
Tải ngay