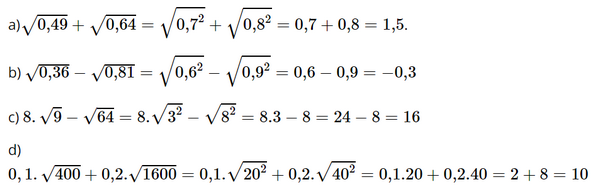Giải Toán 7 trang 35 Cánh Diều tập 1

Bài 1 trang 35 SGK Toán 7 tập 1 - Cánh Diều

a) Đọc các số sau: \(\sqrt {15} ;\sqrt {27,6} ;\sqrt {0,82} \)

b) Viết các số sau: căn bậc hai số học của 39; căn bậc hai số học của \(\frac{9}{{11}}\); căn bậc hai số học của \(\frac{{89}}{{27}}\)

Phương pháp:

\(\sqrt a \) được đọc là căn bậc hai số học của a

Lời giải:

Bài 2 trang 35 SGK Toán 7 tập 1 - Cánh Diều

Chứng tỏ rằng:

a) Số 0,8 là căn bậc hai số học của số 0,64

b) Số -11 không phải là căn bậc hai số học của số 121

c) Số 1,4 là căn bậc hai số học của số 1,96 nhưng –1,4 không phải là căn bậc hai số học của số 1,96.

Phương pháp:

\(\sqrt a  = b\) sao cho \({b^2} = a;b \ge 0\)

Lời giải:

a) Ta có: (0,8)² = 0,8.0,8 = 0,64 và 0,8 > 0 nên số 0,8 là căn bậc hai số học của số 0,64.

b) Ta có: (–11)² = (–11).(–11) = 121 nhưng –11 < 0 nên số –11 không là căn bậc hai số học của số 121.

c) Ta có: (1,4)² = 1,4.1,4 = 1,96 và 1,4 > 0 nên số 1,4 là căn bậc hai số học của số 1,96.

(–1,4)² = (–1,4).(–1,4) = 1,96 nhưng –1,4 < 0 nên số –1,4 không là căn bậc hai số học của số 1,96.

Bài 3 trang 35 SGK Toán 7 tập 1 - Cánh Diều

Tìm số thích hợp cho 

Phương pháp:

+ Tìm căn bậc hai số học của a:

\(\sqrt a  = b\) sao cho \({b^2} = a;b \ge 0\)

+ \(\sqrt a  = b\)thì \(a = {b^2}\)

Lời giải:

Bài 4 trang 35 SGK Toán 7 tập 1 - Cánh Diều

Tính giá trị của biểu thức:

\(\begin{array}{l}a)\sqrt {0,49}  + \sqrt {0,64} ;b)\sqrt {0,36}  - \sqrt {0,81} ;\\c)8.\sqrt 9  - \sqrt {64} ;d)0,1.\sqrt {400}  + 0,2.\sqrt {1600} \end{array}\)

Phương pháp:

\(\sqrt a  = b\) sao cho \({b^2} = a;b \ge 0\)

Lời giải:

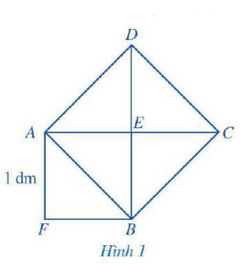
Bài 5 trang 35 SGK Toán 7 tập 1 - Cánh Diều

Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 m, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.

a) Tính diện tích của hình vuông ABCD.

b) Tính độ dài đường chéo AB.

Phương pháp:

a) \({S_{ABCD}} = 4.{S_{AEB}}\)

b) Cạnh x của hình vuông có diện tích S là: \(x = \sqrt S \)

Lời giải:

a) Quan sát Hình 1 ta thấy hình vuông ABCD được tạo thành từ 4 tam giác nhỏ bằng nhau nên diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB. 

Hình vuông AEBF là hình vuông có cạnh bằng 1 và tạo bởi hai tam giác là AEB và AFB nên diện tích của hình vuông AEBF gấp 2 lần diện tích của tam giác AEB.

Diện tích hình vuông AEBF có cạnh bằng 1 m là: 1.1 = 1 (dm²).

 Diện tích hình vuông AEBF gấp 2 lần diện tích tam giác AEB nên diện tích tam giác AEB là: 

 1 : 2 = \(\dfrac{1}{2}\) (dm²). 

Diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB nên diện tích hình vuông ABCD là:

\(\dfrac{1}{2}\) . 4 = 2 (dm²). 

Vậy diện tích hình vuông ABCD là 2 dm².

b) Do √2 là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1, mà hình vuông AEBF có cạnh bằng 1 dm nên đường chéo AB là √2dm

Vậy độ dài đường chéo AB là 

Sachbaitap.com