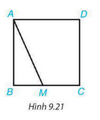
Giải Toán 7 trang 71 Kết nối tri thức với cuộc sống tập 2Giải bài 9.14, 9.15, 9.16, 9.17, 9.18, 9.19 trang 71 SGK Toán lớp 7 kết nối tri thức tập 2. Bài 9.16. Tính chu vi của tam giác cân biết hai cạnh của nó có độ dài là 2 cm và 5 cm. Bài 9.14 trang 71 SGK Toán 7 tập 2 - Kết nối tri thức Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc cạnh CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó. (H.9.21)
Phương pháp: Sử dụng định lí: + Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất. Lời giải:
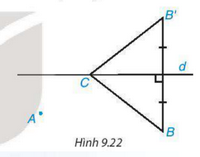
Ta có AB ⊥ BC hay AB ⊥ BM. Vậy AB là khoảng cách từ A đến BC, AM là đường xiên từ A đến bC => AB là đường ngắn nhất và AM > AB Bài 9.15 trang 71 SGK Toán 7 tập 2 - Kết nối tri thức Hỏi có tam giác nào với độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm không? Vì sao? Phương pháp: Kiểm tra tổng độ dài 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất không. Nếu thỏa mãn thì có tam giác có ba cạnh như vậy. Lời giải: Xét theo bất đẳng thức tam gíac, ta có : 2,5 + 3,4 = 5,9 < 6. => Bộ ba độ dài cạnh này không thể tạo thành một tam giác được Bài 9.16 trang 71 SGK Toán 7 tập 2 - Kết nối tri thức Tính chu vi của tam giác cân biết hai cạnh của nó có độ dài là 2 cm và 5 cm. Phương pháp: + Xét 2 trường hợp: cạnh còn lại dài 2 cm hoặc 5 cm + Từ bất đẳng thức tam giác, suy ra độ dài cạnh còn lại. + Chu vi tam giác = Tổng độ dài 3 cạnh Lời giải: Ta có cạnh bên là 5 cm, cạnh đáy là 2 cm vì nó thỏa mãn bất dẳng thức của tam giác: 5+ 5> 2 và 5+2 > 5 Vậy chu vi hình tam giác cân là : 5.2 + 2= 12 (cm) Bài 9.17 trang 71 SGK Toán 7 tập 2 - Kết nối tri thức Độ dài hai cạnh của một tam giác bằng 7 cm và 2 cm. Tính độ dài cạnh còn lại biết rằng số đo của nó theo xentimet là một số tự nhiên lẻ. Phương pháp: Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác) Kết hợp điều kiện độ dài cạnh cần tìm là số tự nhiên lẻ. Lời giải: Gọi độ dài cạnh đó là X Theo bất đẳng thức tam giác, ta có: X < 2+ 7 => X <9 7 < X + 2 => X > 5 Vậy 5 < X < 9. Ta có các số sau : 6,7,8 Theo đề bài, số đo là một số tự nhiên lẻ. Vậy X = 7. Độ dài cần thì là 7 cm Bài 9.18 trang 71 SGK Toán 7 tập 2 - Kết nối tri thức Biết rằng hai cạnh của tam giác có độ dài a và b. Dựa vào bất đẳng thức tam giác, hãy giải thích tại sao chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a+b). Phương pháp: Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác) Chu vi tam giác = Tổng độ dài 3 cạnh Lời giải: Gọi độ dài cạnh còn lại là c. P là chu vi của tam giác Theo bất đẳng thức tam giác, ta có a < b+ c => a+ a < a+ b+ c => 2a < P Theo bất đẳng thức tam giác, ta có : a+ b > c => a + b + a > a+c => 2a + b > a+ c => 2a + b + b > a + c + b => 2a + 2b > a+c +b => 2(a+b) > P Vậy ta có kết luận 2a < P < 2( a+b) Bài 9.19 trang 71 SGK Toán 7 tập 2 - Kết nối tri thức Hai khu vườn A và B nằm về một phía của con kênh d. Hãy xác định bên bờ kênh cùng phía với A và B, một điểm C để đặt máy bơm nước từ kênh tưới cho hai khu vườn sao cho tổng độ dài đường ống dẫn nước từ máy bơm đế hai khu vườn là ngắn nhất .
Phương pháp: Gọi B’ là điểm sao cho d là đường trung trực của BB’. Áp dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại. Lời giải: Ta có: AC + BC ≥ AB (vì C là điểm chưa xác định) Do đó: AC + BC ngắn nhất khi AC + BC = AB => A, B, C thẳng hàng và C nằm giữa A; B. Vậy vị trí để đặt máy bơm nước từ kênh tưới cho hai khu vườn sao cho tổng độ dài đường ống dẫn nước ngắn nhất là C nằm giữa A và B (và A, B, C thẳng hàng) Sachbaitap.com
Xem thêm tại đây:
Luyện tập chung trang 70
|
-

Giải Toán 7 trang 76 Kết nối tri thức với cuộc sống tập 2
Giải bài 9.20, 9.21, 9.22, 9.23, 9.24, 9.25 trang 76 SGK Toán lớp 7 kết nối tri thức tập 2. Bài 9.24. Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.

 Tải ngay
Tải ngay