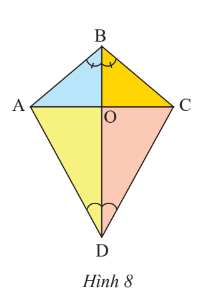
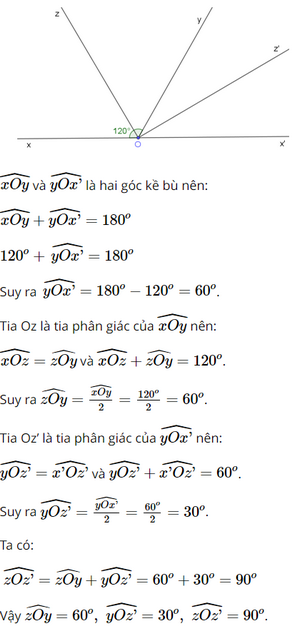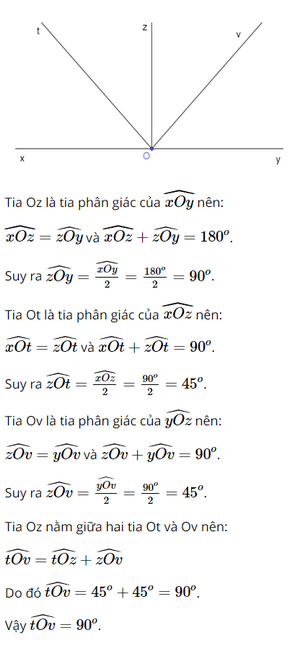Giải Toán 7 trang 75 Chân trời sáng tạo tập 1

Bài 1 trang 75 SGK Toán 7 tập 1 - Chân trời sáng tạo

a) Trong Hình 8, tìm tia phân giác của góc \(\widehat {ABC},\widehat {ADC}\)

b) Cho biết \(\widehat {ABC} = 100^\circ ;\widehat {ADC} = 60^\circ \). Tính số đo của các góc \(\widehat {ABO},\widehat {ADO}\)

Phương pháp:

a) Tia phân giác của một góc là tia xuất phát từ đỉnh của góc, đi qua một điểm trong của góc và tạo với hai cạnh của góc đó hai góc bằng nhau

b) Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\)

Lời giải:

Bài 2 trang 75 SGK Toán 7 tập 1 - Chân trời sáng tạo

a) Vẽ \(\widehat {xOy}\) có số đo là 110 \(^\circ \).

b) Vẽ tia phân giác của \(\widehat {xOy}\) trong câu a

Phương pháp:

Vẽ góc xOy = 110\(^\circ \)

Bước 1: Vẽ góc \(\widehat {xOy} = 110^\circ \). Ta có: \(\widehat {xOz} = \widehat {zOy}\) và \(\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\) nên \(\widehat {xOz} = \frac{{110^\circ }}{2} = 55^\circ \)

Bước 2: Dùng thước đo góc vẽ tia Oz đi qua một điểm trong của \(\widehat {xOy}\)sao cho \(\widehat {xOz} = 55^\circ \)

Ta được Oz là tia phân giác của góc xOy

Lời giải:

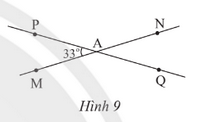
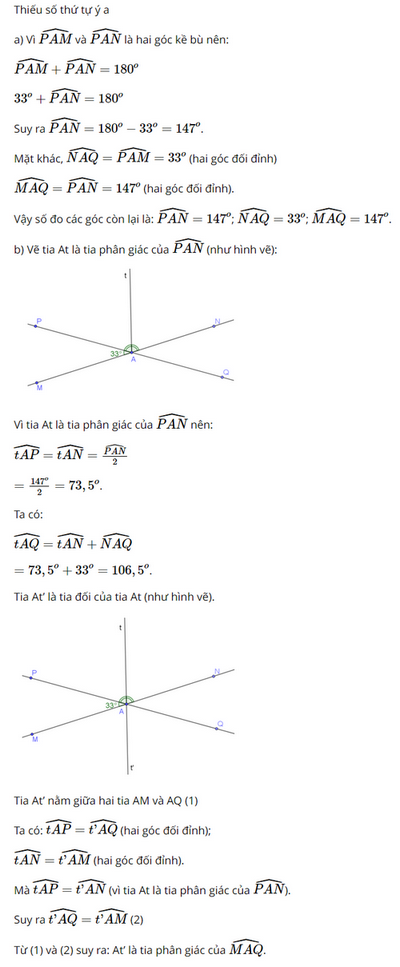
Bài 3 trang 75 SGK Toán 7 tập 1 - Chân trời sáng tạo

Cho đường thẳng MN, PQ cắt nhau tại A và tạọ thành \(\widehat {PAM} = 33^\circ \) (Hình 9)

a) Tính số đo các góc còn lại.

b) Vẽ tia At là tia phân giác của \(\widehat {PAN}\). Hãy tính số đo của \(\widehat {tAQ}\). Vẽ At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của \(\widehat {MAQ}\)

Phương pháp:

Sử dụng tính chất:

+ Hai góc đối đỉnh thì bằng nhau

+ Hai góc kề bù có tổng số đo là 180 độ

+ Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\)

Lời giải:

Bài 4 trang 75 SGK Toán 7 tập 1 - Chân trời sáng tạo

Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho \(\widehat {xOz} = 135^\circ \). Vẽ tia Ot sao cho \(\widehat {yOt} = 90^\circ \) và \(\widehat {zOt} = 135^\circ \). Gọi Ov là tia phân giác của \(\widehat {xOt}\). Các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) có phải là hai góc đối đỉnh không? Vì sao?

Phương pháp:

Vẽ hình

Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\)

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia

Lời giải:

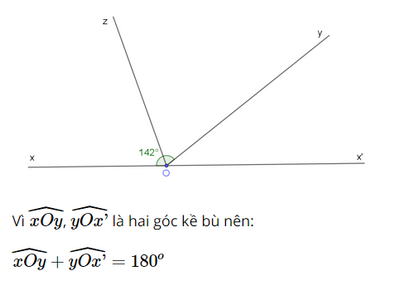
Bài 5 trang 75 SGK Toán 7 tập 1 - Chân trời sáng tạo

Vẽ hai góc kề bù \(\widehat {xOy},\widehat {yOx'}\), biết \(\widehat {xOy} = 142^\circ \). Gọi Oz là tia phân giác của \(\widehat {xOy}\). Tính \(\widehat {x'Oz}\)

Phương pháp:

+ Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\)

+ Hai góc kề bù có tổng số đo là 180 độ

Lời giải:

Bài 6 trang 75 SGK Toán 7 tập 1 - Chân trời sáng tạo

Vẽ hai góc kề bù \(\widehat {xOy},\widehat {yOx'}\), biết \(\widehat {xOy} = 120^\circ \). Gọi Oz là tia phân giác của \(\widehat {xOy}\), Oz’ là tia phân giác của \(\widehat {yOx'}\). Tính \(\widehat {zOy},\widehat {yOz'},\widehat {zOz'}\)

Phương pháp:

+ Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\)

+ Hai góc kề bù có tổng số đo là 180 độ

Lời giải:

Bài 7 trang 75 SGK Toán 7 tập 1 - Chân trời sáng tạo

Vẽ góc bẹt \(\widehat {xOy}\). Vẽ tia phân giác Oz của góc đó. Vẽ tia phân giác Ot của \(\widehat {xOz}\). Vẽ tia phân giác Ov của \(\widehat {zOy}\) . Tính \(\widehat {tOv}\)

Phương pháp:

+ Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\)

+ Hai góc kề bù có tổng số đo là 180 độ

Lời giải:

Sachbaitap.com