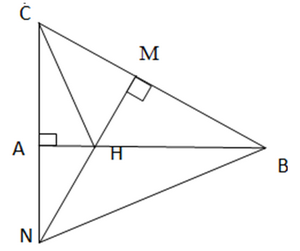
Giải Toán 7 trang 78 Chân trời sáng tạo tập 2Giải bài 1, 2, 3, 4 trang 78 SGK Toán lớp 7 chân trời sáng tạo tập 2. Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng. Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Bài 1 trang 78 SGK Toán 7 tập 2 - Chân trời sáng tạo Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB. Phương pháp: Ta chứng minh H là trực tâm của tam giác NBC Lời giải:
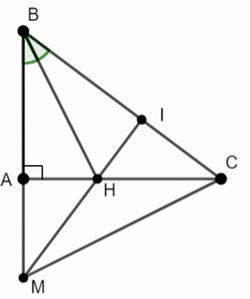
Xét tam giác CNB có : BA ⊥ CA hay BA ⊥ CN => BA là đường cao của tam giác CNB HM ⊥ CB hay NM ⊥ CB => NM là đường cao của tam giác CNB NM giao với BA tại điểm H => H là trực tâm của tam giác CNB => CH ⊥ NB. Bài 2 trang 78 SGK Toán 7 tập 2 - Chân trời sáng tạo Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC. Phương pháp: - Ta chứng minh H là trực tâm của tam giác AMC - Từ đó ta chứng minh MH vuông góc với BC Lời giải:
Bài 3 trang 78 SGK Toán 7 tập 2 - Chân trời sáng tạo Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng: a) DE vuông góc với BC b) BE vuông góc với DC Phương pháp: - Ta chứng minh vuông góc qua các tam giác vuông cân - Ta chứng minh E là trực tâm của tam giác BCD - Từ đó ta chứng minh DE vuông góc với BC và BE vuông góc DC Lời giải:
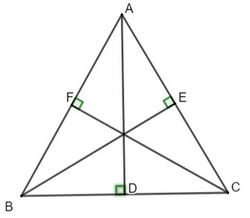
Bài 4 trang 78 SGK Toán 7 tập 2 - Chân trời sáng tạo Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều. Phương pháp: - Ta chứng tam giác BFC = tam giác BEC - Từ đó suy ra góc B = góc C - Chứng minh tương tự suy ra được góc A = góc B = góc C Lời giải:
BE là đường cao của ∆ ABC ⇒ ∆ ABE vuông tại E. CF là đường cao của ∆ ABC ⇒ ∆ AFC vuông tại F. AD là đường cao của ∆ ABC ⇒ ∆ ADC vuông tại D. + Xét ∆ ABE vuông tại E và ∆ AFC vuông tại F có : BE = CF
⇒ ∆ ABE = ∆ AFC (góc nhọn và một cạnh góc vuông). ⇒ AB = AC (1) + Xét ∆CDA vuông tại D và ∆ AFC vuông tại F có : AC chung AD = CF ⇒ ∆CDA = ∆AFC (cạnh huyền và một cạnh góc vuông).
⇒ ∆ ABC cân tại B => AB = BC (2) Từ (1), (2) ta có : AB = AC = BC ⇒ ∆ ABC đều. Sachbaitap.com
Xem thêm tại đây:
Bài 8. Tính chất ba đường cao của tam giác
|
-

Giải Toán 7 trang 81, 82 Chân trời sáng tạo tập 2
Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 81, 82 SGK Toán lớp 7 chân trời sáng tạo tập 2. Bài 2. Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C.

 Tải ngay
Tải ngay