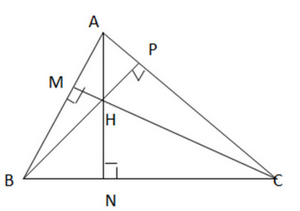
Giải Toán 7 trang 81 Kết nối tri thức với cuộc sống tập 2Giải bài 9.26, 9.27, 9.28, 9.29, 9.30 trang 81 SGK Toán lớp 7 kết nối tri thức tập 2. Bài 9.26. Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB. Bài 9.26 trang 81 SGK Toán 7 tập 2 - Kết nối tri thức Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB. Phương pháp: -Trực tâm của tam giác là giao điểm của ba đường cao -Xác định các đường cao của mỗi tam giác. Lời giải:
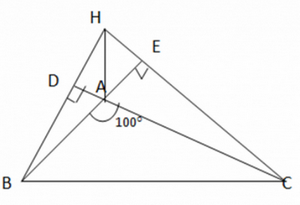
Trong ΔABC ta có H là trực tâm nên: AH ⊥ BC tại N, BH ⊥ AC tại P, CH ⊥ AB tại M Trong ΔAHB, ta có: AC ⊥ BH BC ⊥ AH =>C là trực tâm của tam giác AHB. Trong ΔHAC, ta có: AB ⊥ CH CB ⊥ AH => B là trực tâm của ΔHAC. Trong ΔHBC, ta có: BA ⊥ HC CA ⊥ BH => A là trực tâm của tam giác HBC Bài 9.27 trang 81 SGK Toán 7 tập 2 - Kết nối tri thức Cho tam giác ABC có \(\widehat A = {100^0}\) và trực tâm H. Tìm góc BHC. Phương pháp: - Tính \(\widehat {BAD}\)(Kề bù \(\widehat {BAC}\)) - Tính \(\widehat {ABD}\)(Tam giác ABD vuông tại D) - Tính \(\widehat {BHC}\)(Tam giác BHE vuông tại E) Lời giải:
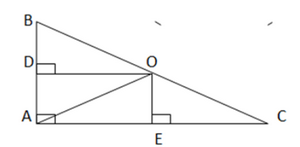
Bài 9.28 trang 81 SGK Toán 7 tập 2 - Kết nối tri thức Xét điểm O cách đều 3 đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông. Phương pháp: Chứng minh tam giác ABC có một góc bằng 90 độ Lời giải:
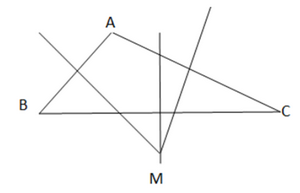
Bài 9.29 trang 81 SGK Toán 7 tập 2 - Kết nối tri thức a) Có một chi tiết máy ( đường viền ngoài là đường tròn) bị gãy. (H.9.46). Làm thế nào để xác định được bán kính của đường viền này ? b) Trên bản đồ, ba khu dân cư được quy hoạch tại điểm A, B, C không thẳng hàng. Hãy tìm trên bản đồ một điểm M cách đều A, B, C để quy hoạch một trường học
Phương pháp: a) Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy sau đó xác định giao điểm 3 đường trung trực của đoạn AB, BC, CA. b) Vẽ đường trung trực của các đoạn AB, AC, BC. Lời giải: a)
Ta có hình vẽ minh họa
b)
Ta có hình minh họa
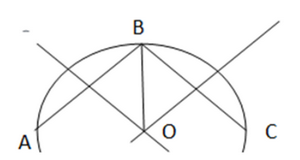
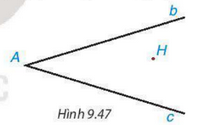
Bài 9.30 trang 81 SGK Toán 7 tập 2 - Kết nối tri thức Cho hai đường thẳng không vuông góc b,c cắt nhau tại điểm A và cho điểm H không thuộc b và c (H.9.47). Hãy tìm điểm B thuộc b, điểm C thuộc c sao cho tam giác ABC nhận H làm trực tâm.
Phương pháp: Để vẽ trực tâm ta xác định 2 đường cao của tam giác trên. Giao điểm của 2 đường cao chính là trực tâm của tam giác. Lời giải: Kẻ HD ⊥ đường thẳng c tại điểm D, HE⊥ đường thẳng b tại điểm E Nối A với H. Lấy điểm B thuộc đường thẳng b sao cho BE nằm giữa B và A Từ B kẻ đường vuông góc với AH, đường thẳng đó cắt đường thẳng c tại 1 điểm. Điểm đó chính là điểm C => H là trực tâm của tam giác ABC
Sachbaitap.com
|
-

Giải Toán 7 trang 83 Kết nối tri thức với cuộc sống tập 2
Giải bài 9.31, 9.32, 9.33, 9.34, 9.35 trang 81 SGK Toán lớp 7 kết nối tri thức tập 2. Bài 9.33. Có một mảnh tôn hình tròn cần đục lỗ ở tâm. Làm thế nào để xác định được tâm của mảnh tôn đó?

 Tải ngay
Tải ngay