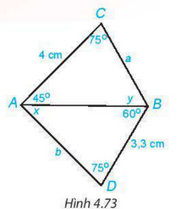
Giải Toán 7 trang 86 Kết nối tri thức với cuộc sống tập 1Giải bài 4.29, 4.30, 4.31, 4.32 trang 86 SGK Toán lớp 7 tập 1 kết nối tri thức với cuộc sống. Bài 4.29. Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ. Bài 4.29 trang 86 SGK Toán 7 tập 1 - Kết nối tri thức Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ.
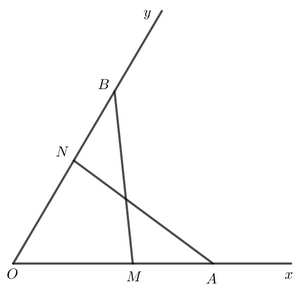
Phương pháp: Áp dụng tổng ba góc trong một tam giác bằng 180 độ để tìm x,y. Chứng minh 2 tam giác bằng nhau để tìm a,b. Lời giải: Xét tam giác ABC có: \(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat C = {180^o}\\ \Rightarrow {45^o} + y + {75^o} = {180^o}\\ \Rightarrow y = {60^o}\end{array}\) Xét tam giác ABD có: \(\begin{array}{l}\widehat {DAB} + \widehat {DBA} + \widehat D = {180^o}\\ \Rightarrow x + {60^o} + {75^o} = {180^o}\\ \Rightarrow x = {45^o}\end{array}\) Xét 2 tam giác ABC và ADB có: \(\widehat {DAB} = \widehat {CAB} = {45^o}\) AB chung \(\widehat D = \widehat C = {75^o}\) =>\(\Delta ABC = \Delta ADB\)(g.c.g) =>BC=BD ( 2 cạnh tương ứng), mà BD = 3,3 cm =>a= BC= 3,3cm AC=AD ( 2 cạnh tương ứng), mà AC = 4 cm =>b = AD = 4cm Bài 4.30 trang 86 SGK Toán 7 tập 1 - Kết nối tri thức Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM. Chứng minh rằng: a) \(\Delta \)OAN = \(\Delta \)OBM; b) \(\Delta \)AMN = \(\Delta \)BNM. Phương pháp: Chứng minh 2 tam giác bằng nhau theo trường hợp cạnh-góc-cạnh. Lời giải: a)
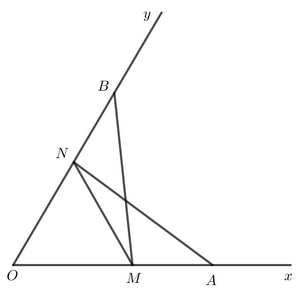
 b)
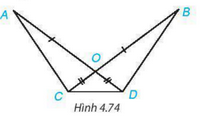
Do ΔOAN=ΔOBM">ΔOAN=ΔOBM nên AN = BM (2 cạnh tương ứng). Có BN = OB – ON, AM = OA – OM. Mà OB = OA, ON = OM nên BN = AM. Xét hai tam giác AMN và BNM có: AM = BN (chứng minh trên). MN chung. AN = BM (chứng minh trên). Vậy ΔAMN=ΔBNM">ΔAMN=ΔBNM (c – c – c). Bài 4.31 trang 86 SGK Toán 7 tập 1 - Kết nối tri thức Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng: a) AC = BD; b) \(\Delta \)ACD = \(\Delta \)BDC.
Phương pháp: a) Chứng minh 2 tam giác ACD và BDC bằng nhau. b) Chỉ ra 3 cạnh của hai tam giác đó bằng nhau Lời giải:
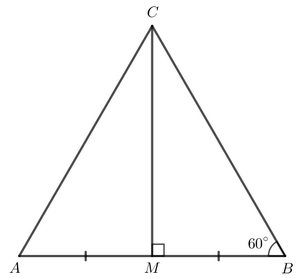
Bài 4.32 trang 86 SGK Toán 7 tập 1 - Kết nối tri thức Cho tam giác MBC vuông tại M có \(\widehat B\) = 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều. Phương pháp: Chứng minh tam giác ABC cân tại C và có 1 góc bằng 60 độ. Lời giải:
Xét hai tam giác AMC vuông tại M và BMC vuông tại M có: AM = BM (theo giả thiết). MC chung. Do đó ΔAMC=ΔBMC">ΔAMC=ΔBMCΔAMC=ΔBMC (2 cạnh góc vuông). Khi đó AC = BC (2 cạnh tương ứng). Tam giác ABC có AC = BC nên tam giác ABC cân tại C. Tam giác ABC cân tại C lại có Vậy tam giác ABC là tam giác đều. Sachbaitap.com
Xem thêm tại đây:
Luyện tập chung trang 85
|
-

Giải Toán 7 trang 87 Kết nối tri thức với cuộc sống tập 1
Giải bài 4.33, 4.34, 4.35, 4.36, 4.37, 4.38, 4.39 trang 87 SGK Toán lớp 7 kết nối tri thức tập 1. Bài 4.33. Tính các số đo x, y trong tam giác dưới đây (H.4.75)

 Tải ngay
Tải ngay