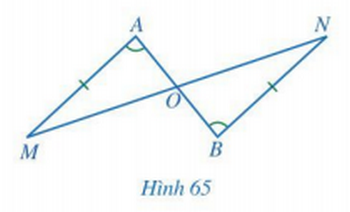
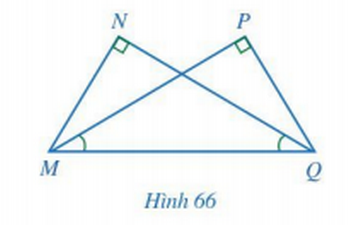
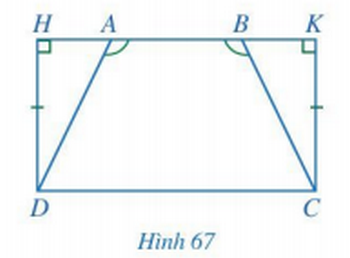
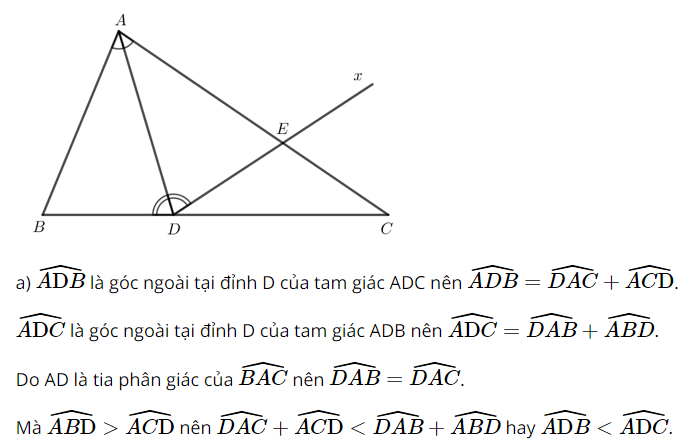
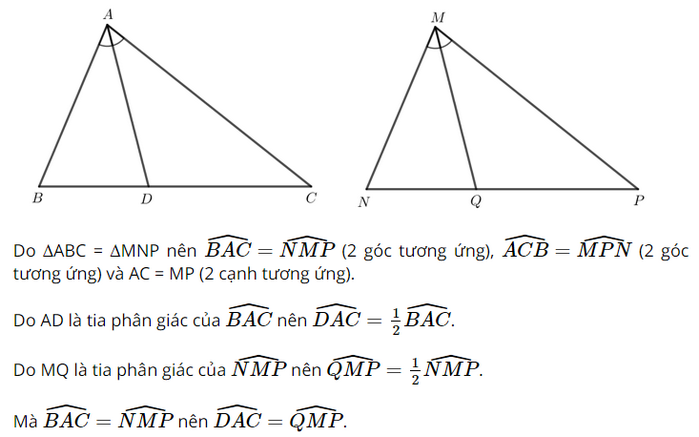
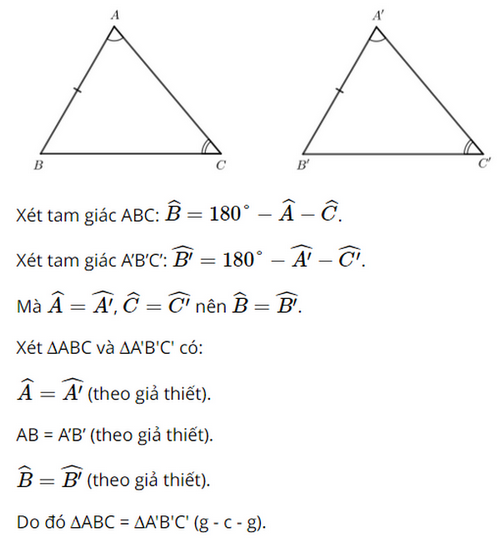Giải Toán 7 trang 91, 92 Cánh Diều tập 2Giải bài 1, 2 trang 91, bài 3, 4, 5, 6 trang 92 SGK Toán lớp 7 cánh diều tập 2. Cho ∆ABC = ∆MNP. Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ. Bài 1 trang 91 SGK Toán 7 tập 2 - Cánh Diều Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’, \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao? Phương pháp: So sánh hai tam giác ABC và A’B’C’. Tổng ba góc trong một tam giác bằng 180°. Lời gải: Bài 2 trang 91 SGK Toán 7 tập 2 - Cánh Diều Cho Hình 65 có AM = BN, \(\widehat A = \widehat B\). Chứng minh: OA = OB, OM = ON. Phương pháp: Chứng minh tam giác AOM bằng tam giác BON. Lời giải: Suy ra ∆AOM = ∆BON (g - c - g). Do đó OA = OB (2 cạnh tương ứng), OM = ON (2 cạnh tương ứng). Bài 3 trang 92 SGK Toán 7 tập 2 - Cánh Diều Cho Hình 66 có \(\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}\). Chứng minh MN = QP, MP = QN. Phương pháp: Chứng minh hai tam giác MNQ bằng tam giác QPM. Lời giải: MQ chung. Suy ra ∆MNQ = ∆QPM (cạnh huyền - góc nhọn). Do đó MN = QP (2 cạnh tương ứng), MP = QN (2 cạnh tương ứng). Bài 4 trang 92 SGK Toán 7 tập 2 - Cánh Diều Cho Hình 67 có \(\widehat {AHD} = \widehat {BKC} = 90^\circ ,DH = CK,\widehat {DAB} = \widehat {CBA}\). Chứng minh AD = BC. Phương pháp: Chứng minh tam giác AHD bằng tam giác BKC. Lời giải: DH = CK (theo giả thiết). Suy ra ∆AHD = ∆BKC (góc nhọn - cạnh góc vuông). Do đó AD = BC (2 cạnh tương ứng). Bài 5 trang 92 SGK Toán 7 tập 2 - Cánh Diều Cho tam giác ABC có \(\widehat B > \widehat C\). Tia phân giác góc BAC cắt cạnh BC tại điểm D. a) Chứng minh \(\widehat {ADB} < \widehat {ADC}\). b) Kẻ tia Dx nằm trong góc ADC sao cho \(\widehat {ADx} = \widehat {ADB}\). Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: \(\Delta ABD = \Delta AED,AB < AC\). Phương pháp: a) Tổng ba góc trong một tam giác bằng 180°. b) Chứng minh \(\Delta ABD = \Delta AED\) theo trường hợp g.c.g và AB < AC vì cạnh đối diện với góc lớn hơn thì lớn hơn. Lời giải: b) Xét ∆ABD và ∆AED có: Suy ra ∆ABD = ∆AED (g - c - g). Do đó AB = AE. Mà AE < AC nên AB < AC. Vậy ∆ABD = ∆AED và AB < AC. Bài 6 trang 92 SGK Toán 7 tập 2 - Cánh Diều Cho \(\Delta ABC = \Delta MNP\). Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ. Phương pháp: Chứng minh tam giác ABD bằng tam giác MNQ. Lời giải: Xét ∆ADC và ∆MQP có: Suy ra ∆ADC = ∆MQP (g - c - g). Do đó AD = MQ (2 cạnh tương ứng). Sachbaitap.com
|
-

Giải Toán 7 trang 96 Cánh Diều tập 2
Giải bài 1, 2, 3, 4, 5 trang 96 SGK Toán lớp 7 cánh diều tập 2. Cho tam giác ABC cân tại A có M là trung điểm cạnh AC và N là trung điểm cạnh AB. Chứng minh (BM = CN)

 Tải ngay
Tải ngay