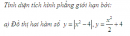Từ câu 3.55 đến câu 3.62 trang 150 đến trang 151 sách bài tập Giải tích 12 Nâng caoHãy chọn một trong bốn phương án đã cho để được khẳng định đúng. Câu 3.55 trang 150 sách bài tập Giải tích 12 Nâng cao (A) \(f\left( x \right) = {e^{2x}}\) (B) \(f\left( x \right) = 2x{e^{{x^2}}}\) (C) \(f\left( x \right) = {{{e^{{x^2}}}} \over {2x}}\) (D) \(f\left( x \right) = {x^2}{e^{{x^2}}} - 1\) Giải Chọn B Câu 3.56 trang 150 sách bài tập Giải tích 12 Nâng cao Cho đồ thị hàm số \(y = f\left( x \right)\) . Diện tích hình phẳng (phần tô đậm trong hình 3.1) là: (A) \(\int\limits_{ - 3}^4 {f\left( x \right)} dx\) (B) \(\int\limits_{ - 3}^1 {f\left( x \right)} dx + \int\limits_1^4 {f\left( x \right)} dx\) (C) \(\int\limits_{ - 3}^0 {f\left( x \right)} dx + \int\limits_4^0 {f\left( x \right)} dx\) (D) \(\int\limits_0^{ - 3} {f\left( x \right)} dx + \int\limits_0^4 {f\left( x \right)} dx\) Giải Chọn C Câu 3.57 trang 151 sách bài tập Giải tích 12 Nâng cao Giả sử \(\int\limits_1^5 {{{dx} \over {2x - 1}}} = \ln K\). Giá trị của K là (A) 9 (B) 3 (C) 81 (D) 8 Giải Chọn B Câu 3.58 trang 151 sách bài tập Giải tích 12 Nâng cao Cho \(I = \int\limits_1^2 {2x\sqrt {{x^2} - 1} dx} \) và \(u = {x^2} - 1\). Chọn khẳng đinh sai trong các khẳng định sau: (A) \(I = \int\limits_0^3 {\sqrt u } du\) (B) \(I = {2 \over 3}\sqrt {27} \) (C) \(I = \int\limits_1^2 {\sqrt u } du\) (D) \(I = {2 \over 3}{u^{{3 \over 2}}}\left| {_0^3} \right.\) Giải Chọn C Câu 3.59 trang 151 sách bài tập Giải tích 12 Nâng cao Cho \(I = \int\limits_0^{{\pi \over 6}} {\sin x\cos xdx} = {1 \over {64}}.\) Khi đó n bằng (A) 6 (B) 5 (C) 4 (D) 3 Giải Chọn D Câu 3.60 trang 151 sách bài tập Giải tích 12 Nâng cao Giá trị của \(\int\limits_0^2 {2{e^{2x}}} dx\) bằng (A) \({e^4}\) (B) \({e^4} - 1\) (C) \(4{e^4}\) (D) \(3{e^4}\) Giải Chọn B Câu 3.61 trang 151 sách bài tập Giải tích 12 Nâng cao Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2}\) và đường thẳng \(y = 2x\) là: (A) \({4 \over 3}\) (B) \({3 \over 2}\) (C) \({5 \over 3}\) (D) \({{23} \over {15}}\) Giải Chọn A Câu 3.62 trang 151 sách bài tập Giải tích 12 Nâng cao Giả sử \(\int\limits_{ - 2}^2 {f\left( x \right)} dx = 4,\int\limits_2^5 {f\left( x \right)} dx = 3,\int\limits_{ - 2}^5 {g\left( x \right)} dx = 6\). Khẳng định sau đây đúng hay sai:\(f\left( x \right) \le g\left( x \right)\) với mọi \(x \in \left[ { - 2;5} \right]\) Giải Sai. \(\int\limits_{ - 2}^5 {f\left( x \right)} dx = 4 + 3 = 7;\int\limits_{ - 2}^5 {g\left( x \right)} dx = 6\) nên \(\int\limits_{ - 2}^5 {f\left( x \right)} dx > \int\limits_{ - 2}^5 {g\left( x \right)} dx\) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
|
-

Câu 3.72 trang 154 sách bài tập Giải tích 12 Nâng cao
Tính thể tích khối tròn xoay tạo thành khi quay quanh trục tung mỗi hình phẳng giới hạn bởi các đường sau:

 Tải ngay
Tải ngay