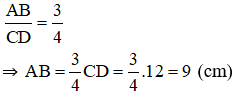Bài 1, 2, 3, 4, 5 trang 58, 59 SGK Toán 8 tập 2 - Định lí Ta-lét trong tam giácBài 1 trang 58; bài 2, 3, 4, 5 trang 59 SGK Toán 8 tập 2 - Định lí Ta-lét trong tam giác. Bài 3 Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B'. Bài 1 trang 58 SGK Toán lớp 8 tập 2 Câu hỏi: Viết tỉ số của các cặp đoạn thẳng có độ dài như sau: a. \(AB = 5cm\) và \(CD =15 cm\); b.\(EF = 48 cm\) và \(GH = 16 dm\); c. \(PQ = 1,2m\) và \(MN = 24 cm\). Phương pháp: Áp dụng định nghĩa: Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo. Tỉ số của a và b là \(\dfrac{a}{b}\) Lời giải:
Bài 2 trang 59 SGK Toán lớp 8 tập 2 Câu hỏi: Cho biết \(\dfrac{AB}{CD} = \dfrac{3}{4}\) và \(CD= 12cm\). Tính độ dài \(AB\). Phương pháp: Áp dụng tính chất của hai tỉ số bằng nhau. \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow ad = bc\) Lời giải: Thay CD = 12cm vào tỉ số độ dài ta được:
Vậy độ dài AB = 9cm Bài 3 trang 59 SGK Toán lớp 8 tập 2 Câu hỏi: Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B'. Phương pháp: - Biểu diễn độ dài của đoạn thẳng \(AB\) và \(A'B'\) theo \(CD\). Sau đó lập tỉ số. Lời giải: Theo đề bài ta có: \(AB= 5CD\); \(A'B'= 12CD\). \( \Rightarrow \) Tỉ số của hai đoạn thẳng \(AB\) và \(A'B'\) là: \(\dfrac{AB}{A'B'}= \dfrac{5CD}{12CD} = \dfrac{5}{12}\) Bài 4 trang 59 SGK Toán lớp 8 tập 2 Câu hỏi:
Phương pháp: - Áp dụng định lí TaLet và tính chất dãy tỉ số bằng nhau. Lời giải: a. Ta có: \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\) (giả thiết) \( \Rightarrow \dfrac{AC}{AC'}=\dfrac{AB}{AB'}\) \( \Rightarrow \dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AB}}{{AB'}} - 1\) Ta có: \(\dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AC - AC'}}{{AC'}} = \dfrac{{C'C}}{{AC'}}\) \(\dfrac{{AB}}{{AB'}} - 1 = \dfrac{{AB - AB'}}{{AB'}} = \dfrac{{B'B}}{{AB'}}\) \( \Rightarrow \dfrac{{C'C}}{{AC'}} = \dfrac{{B'B}}{{AB'}} \Rightarrow \dfrac{{AB'}}{{B'B}} = \dfrac{{AC'}}{{C'C}}\) (điều phải chứng minh). b. Vì \(\dfrac{AB'}{AB} = \dfrac{AC'}{AC}\) Mà \(AB' = AB - B'B, AC' = AC - C'C\) \(\dfrac{AB-BB'}{AB} = \dfrac{AC -CC'}{AC}\) \( \Rightarrow 1 - \dfrac{{BB'}}{{AB}} = 1 - \dfrac{{CC'}}{{AC}}\) \( \Rightarrow \dfrac{BB'}{AB}= \dfrac{CC'}{AC}\) (điều phải chứng minh). Bài 5 trang 59 SGK Toán lớp 8 tập 2 Câu hỏi:
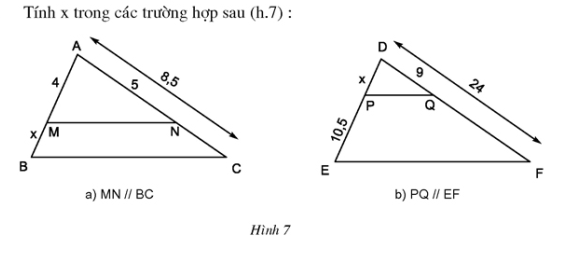
Phương pháp: Áp dụng định lý Ta-let trong tam giác. Lời giải: a) \(MN // BC\) (giả thiết) Theo định lí Ta-lét ta có: \( \dfrac{BM}{AM} = \dfrac{CN}{AN}\) Mà \(CN =AC- AN= 8,5 - 5= 3,5\) Ta được \(\dfrac{x}{4}= \dfrac{3,5}{5} \Rightarrow x = \dfrac{4.3,5}{5} = 2,8\). Vậy \(x = 2,8\). b) \(PQ // EF\) (giả thiết) Theo định lí Ta-lét ta có: \( \dfrac{DP}{PE} = \dfrac{DQ}{QF}\) Mà \(QF = DF - DQ = 24 - 9 = 15\) Ta được \(\dfrac{x}{10,5} = \dfrac{9}{15} \Rightarrow x = \dfrac{10,5.9}{15} = 6,3\) Vậy \(x=6,3\). sachbaitap.com
Xem thêm tại đây:
Chương III. Tam giác đồng dạng
|
-

Bài 6, 7, 8, 9 trang 62, 63 SGK Toán 8 tập 2 - Định lí đảo và hệ quả của định lí Ta-lét
Bài 6, 7 trang 62, bài 8, 9 trang 63 SGK Toán 8 tập 2 - Định lí đảo và hệ quả của định lí Ta-lét. Bài 9 Cho tam giác ABC và điểm D trên cạnh AB sao cho AD = 13,5cm, DB = 4,5cm. Tính tỉ số các khoảng cách từ các điểm D và B đến cạnh AC.
-

Bài 10, 11, 12, 13, 14 trang 63, 64 SGK Toán 8 tập 2 - Luyện tập
Bài 10, 11 trang 63; bài 12, 13, 14 trang 64 SGK Toán 8 tập 2 - Luyện tập. Bài 10 Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H' (h.16).
-

Bài 15, 16, 17, 18, 19, 20, 21, 22 trang 67, 68 SGK Toán 8 tập 2 - Tính chất đường phân giác của tam giác - Luyện tập
Bài 15, 16 trang 67; bài 17, 18, 19, 20, 21, 22 trang 68 SGK Toán 8 tập 2 - Tính chất đường phân giác của tam giác - Luyện tập. Bài 20 Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O.
-

Bài 23, 24, 25, 26, 27, 28 trang 71, 72 SGK Toán 8 tập 2 -Khái niệm hai tam giác đồng dạng- Luyện tập
Bài 23 trang 71, bài 24, 25, 26, 27, 28 trang 72 SGK Toán 8 tập 2 -Khái niệm hai tam giác đồng dạng- luyện tập. Bài 23 Trong hai mệnh đề sau đây, mệnh đề nào đúng? Mệnh đề nào sai? a) Hai tam giác bằng nhau thì đồng dạng với nhau.

 Tải ngay
Tải ngay