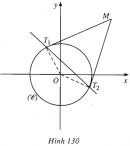
Bài 103 trang 122 SBT Hình học 10 Nâng cao

Cho đường tròn \((C): {x^2} + {y^2} - 8x - 6y + 21 = 0\) và điểm \(M(4 ; 5).\)

a) Chứng minh rằng điểm \(M\) nằm trên đường tròn \((C)\). Viết phương trình tiếp tuyến của \((C)\) tại \(M;\)

b) Viết phương trình đường tròn đối xứng với \((C)\) qua đường thẳng \(y=x.\)

Giải

a) \((C)\) có tâm \(I(4 ; 3)\), bán kính \(R=2\). Dễ  thấy tọa độ của M thỏa mãn phương trình của \((C)\) nên \(M\) nằm trên \((C)\). Ta cũng viết được phương trình của \((C)\) tại \(M\) là \(y-5=0.\)

b) Đường tròn \((C’)\) đối xứng với \((C)\) qua đường thẳng \(\Delta : y = x\) khi \((C’)\) có bán kính bằng \(2\) và có tâm \(I’\) đối xứng với \(I\) qua \(\Delta \). Ta tìm được \(I’=(3 ; 4)\) và viết được phương trình của \((C’)\) là \({(x - 3)^2} + {(y - 4)^2} = 4\).

Sachbaitap.com