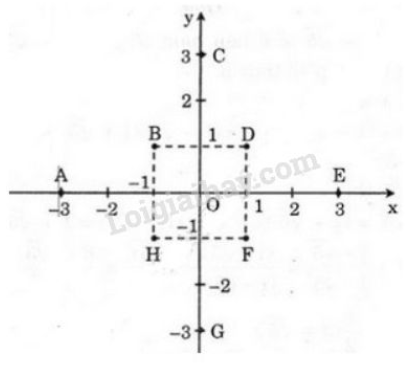
Bài 11, 12, 13, 14 trang 48 SGK Toán 9 tập 1 - Luyện tập

Bài 11 trang 48 SGK Toán lớp 9 tập 1

Câu hỏi:

Hãy biểu biễn các điểm sau trên mặt phẳng tọa độ:

\(A(-3; 0)\),  \(B(-1; 1)\),  \(C(0; 3)\),   \(D(1; 1)\), 

\(E(3; 0)\),   \(F(1; -1)\),  \(G(0; -3)\),  \(H(-1; -1)\).

Phương pháp:

+) Điểm \(A(x_0; y_0)\) thì hoành độ là \(x_0\) và tung độ là \(y_0\).

+) Điểm \(B(0; b)\) nằm trên trục tung, tung độ là \(b\).

+) Điểm \(C(c; 0)\) nằm trên trục hoành, tung độ là \(c\).

Lời giải:

+) Điểm \(A(-3; 0) \Rightarrow\) hoành độ là \(-3\) và tung độ là \(0\)

\(\Rightarrow \) điểm \(A\) nằm trên trục hoành, hoành độ là \(-3\).

+) Điểm \(B(-1; 1) \Rightarrow\) hoành độ là \(-1\) và tung độ là \(1\)

+) Điểm \(C(0; 3) \Rightarrow\) hoành độ là \(0\) và tung độ là \(3\)

\(\Rightarrow \) điểm \(C\) nằm trên trục tung, tung độ là \(3\).

+) Điểm \(D(1; 1)  \Rightarrow\) hoành độ là \(1\) và tung độ là \(1\)

+) Điểm \(E(3; 0) \Rightarrow\) hoành độ là \(3\) và tung độ là \(0\)

\(\Rightarrow \) điểm \(E\) nằm trên trục hoành, hoành độ là \(3\).

+) Điểm \(F(1; -1) \Rightarrow\) hoành độ là \(1\) và tung độ là \(-1\)

+) Điểm \(G(0; -3) \Rightarrow\) hoành độ là \(0\) và tung độ là \(-3\)

\(\Rightarrow \) điểm \(C\) nằm trên trục tung, tung độ là \(-3\).

+) Điểm \(H(-1; -1) \Rightarrow\) hoành độ là \(-1\) và tung độ là \(-1\)

Xem hình sau:

Bài 12 trang 48 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho hàm số bậc nhất y = ax + 3. Tìm hệ số a, biết rằng khi x = 1 thì y = 2,5. 

Lời giải: 

Thay \(x=1,\ y=2,5\) vào công thức hàm số \(y = ax + 3\), ta được:

\( 2,5=1.a+3 \) 

\(\Leftrightarrow 2,5= a+3 \)

\(\Leftrightarrow 2,5-3 = a\)

\(\Leftrightarrow a=-0,5\).

Vậy \(a=-0,5\) và hàm số đó là \(y=-0,5x+3\).

Bài 13 trang 48 SGK Toán lớp 9 tập 1

Câu hỏi:

Với những giá trị nào của \(m\) thì mỗi hàm số sau là hàm số bậc nhất ?

a) \(y=\sqrt{5 - m}(x - 1)\);

b) \(y = \dfrac{m + 1}{m - 1}x +3,5\)

Lời giải:

 a) Ta có \(y=\sqrt{5 - m}(x - 1) \Leftrightarrow  y=\sqrt{5 - m}.x - \sqrt{5 - m} \)

     \(\Rightarrow\) Hệ số là \(a=\sqrt{5-m}\).

Điều kiện để  \(y=\sqrt{5 - m}.x - \sqrt{5 - m}\) là hàm số hàm bậc nhất là: 

\(\left\{ \matrix{
\sqrt {5 - m} \ne 0 \hfill \cr
5-m \ge 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
5-m \ne 0 \hfill \cr
5-m\ge 0 \hfill \cr} \right.\)

\(\Leftrightarrow  5-m > 0 \Leftrightarrow m < 5\)

Vậy \( m < 5\) thì hàm số đã cho là hàm số bậc nhất.

b) Ta có: \(y = \dfrac{m + 1}{m - 1}x +3,5 \Rightarrow\) Hệ số \(a=\dfrac{m + 1}{m - 1}\) 

Điều kiện để hàm số \(y = \dfrac{m + 1}{m - 1}x +3,5\) là hàm bậc nhất là: 

\(\left\{ \matrix{
\dfrac{m + 1}{m - 1} \ne 0 \hfill \cr
m - 1 \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
m + 1 \ne 0 \hfill \cr
m - 1 \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
m \ne - 1 \hfill \cr
m \ne 1 \hfill \cr} \right.\)

Vậy \( m \ne \pm 1\) thì hàm số đã cho là hàm số bậc nhất.

Bài 14 trang 48 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho hàm số bậc nhất \(y = (1 - \sqrt{5}) x - 1\).

a) Hàm số trên là đồng biến hay nghịch biến trên \(\mathbb{R}\) ? Vì sao ?

b) Tính giá trị của \(y\) khi \(x = 1 + \sqrt{5}\);

c) Tính giá trị của \(x\) khi \(y=\sqrt{5}\). 

Phương pháp:

a) +) Hàm số bậc nhất \(y=ax+b\) xác định với mọi giá trị của \(x\) trên \(\mathbb{R}\)

  -  Đồng biến trên \(\mathbb{R}\)  khi \( a > 0\). 

  -  Nghịch biến trên \(\mathbb{R}\)  khi \(a < 0\).

+) Sử dụng định lí so sánh hai căn bậc hai số học của hai số không âm:

            \(a < b \Leftrightarrow  \sqrt a < \sqrt b,\)  với \(a,\ b \ge 0\).

b) +) Thay \(x_0\) vào công thức hàm số \(y=ax+b\) tính được giá trị của hàm số: \(y_0=ax_0+b\).

     +) Sử dụng hằng đẳng thức: \(  a^2-b^2=(a-b)(a+b).\)

c) +) Thay \(x_0\) vào công thức hàm số \(y=ax+b\) tính được giá trị của hàm số: \(y_0=ax_0+b\).

     +) Sử dụng hằng đẳng thức:

            \( (a+b)^2=a^2+2ab+b^2\).

            \(  a^2-b^2=(a-b)(a+b).\)

+) Sử dụng công thức trục căn thức ở mẫu:

        \(\dfrac{C}{\sqrt A \pm B}=\dfrac{C(\sqrt A \mp B)}{A - B^2}\)

Lời giải:

a) Hàm số \(y = (1 - \sqrt{5}) x - 1\) có hệ số \(a=1-\sqrt 5<0\)

(Vì: \(1 < 5 \Leftrightarrow \sqrt 1<\sqrt{5}\) \(\Leftrightarrow 1<\sqrt{5}\)\(\Leftrightarrow 1-\sqrt{5}<0)\)

Vậy hàm số \(y = (1 - \sqrt{5}) x - 1\) nghịch biến trên \(\mathbb{R}\) (vì hệ số \(a\) âm).

b) 

Thay \(x = 1 + \sqrt{5}\) vào công thức của hàm số đã cho, ta được: 

           \( y=(1-\sqrt{5})(1+\sqrt{5})-1\)

       \(\Leftrightarrow y= [1^2 -(\sqrt 5)^2]-1\)

      \(\Leftrightarrow y= (1-5)-1\)

      \(\Leftrightarrow y= -4-1\)

      \(\Leftrightarrow y= -5\)

Vậy \(x = 1 + \sqrt{5}\) thì \(y= -5\).

c) Ta có:

Thay \(y=\sqrt{5}\) vào công thức của hàm số, ta được:

\(\sqrt{5}=(1-\sqrt{5})x-1 \)

\(\Leftrightarrow (1-\sqrt 5)x=\sqrt 5 +1\)

\(\Leftrightarrow x=\dfrac{\sqrt 5 +1}{1-\sqrt 5}\)

\(\Leftrightarrow x=\dfrac{(\sqrt 5 +1)(\sqrt 5 +1)}{(1-\sqrt 5)(\sqrt 5 +1)}\)

\(\Leftrightarrow x = \dfrac{(\sqrt 5 +1)^2}{1^2-(\sqrt 5)^2}\)

\(\Leftrightarrow x = \dfrac{(\sqrt 5)^2+2\sqrt 5 +1}{1-5}\)

\(\Leftrightarrow x = \dfrac{ 5+2\sqrt 5 +1}{-4}\)

\(\Leftrightarrow x = -\dfrac{ 6+2\sqrt 5 }{4}\)

\(\Leftrightarrow x = -\dfrac{ 2(3+\sqrt 5)}{2.2}\)

\(\Leftrightarrow x = -\dfrac{ 3+\sqrt 5 }{2}\)

Vậy \(y=\sqrt 5\) thì \(x=-\dfrac{3+\sqrt 5}{2}\).

Sachbaitap.com