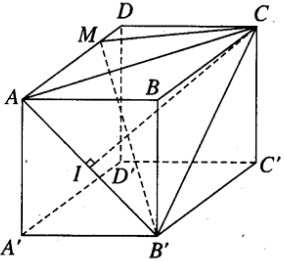
Bài 1.14 trang 20 sách bài tập (SBT) – Hình học 12Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = 2a, AA’ = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = 2a, AA’ = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD. a) Tính thể tích khối chóp M.AB’C b) Tính khoảng cách từ M đến mặt phẳng (AB’C). Hướng dẫn làm bài:
a) Thể tích khối chóp M.AB’C bằng thể tích khối chóp B’AMC. Ta có: \({S_{AMC}} = {3 \over 4}{S_{ADC}} = {3 \over 4}.{1 \over 2}.2{a^2} = {{3{a^2}} \over 4}\) Do đó \({V_{M.AB'C}} = {1 \over 3}.{{3{a^2}} \over 4}.a = {{{a^3}} \over 4}\) b) Gọi h là khoảng cách từ M đến mặt phẳng (AB’C) Khi đó \({V_{M.AB'C}} = {1 \over 3}{S_{AB'C}}.h = {{{a^3}} \over 4}\) Vì AC2 = B’C2 = 5a2 nên tam giác ACB’ cân tại C. Do đó, đường trung tuyến CI của tam giác ACB’ cũng là đường cao. Ta có: \(C{I^2} = {\rm{ }}C{A^2}-{\rm{ }}A{I^2} = {\rm{ }}5{a^2} - {({{a\sqrt 2 } \over 2})^2} = 5{a^2} - {{{a^2}} \over 2} = {{9{a^2}} \over 2}\) Do đó \(CI = {{3a} \over {\sqrt 2 }}\Rightarrow {S_{AB'C}} = {1 \over 2}.{{3a} \over {\sqrt 2 }}.a\sqrt 2 = {{3{a^2}} \over 2}\) Từ đó suy ra \(h = 3{{{a^3}} \over 4}:{{3{a^2}} \over 2} = {a \over 2}\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 3. Khái niệm về thể tích khối đa diện
|
-
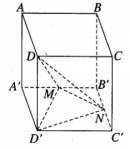
Bài 1.15 trang 21 sách bài tập (SBT) – Hình học 12
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’
-
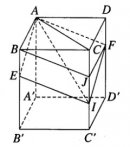
Bài 1.16 trang 21 sách bài tập (SBT) – Hình học 12
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho.
-
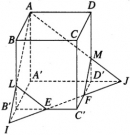
Bài 1.17 trang 21 sách bài tập (SBT) – Hình học 12
Cho hình hộp ABCD.A’B’C’D’. Gọi E và F lần lượt là trung điểm của B’C’ và C’D’.
-
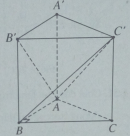
Bài 1.25 trang 21 sách bài tập (SBT) – Hình học 12
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông ở B, AB = BC = AA’. Hãy chia lăng trụ đó thành ba tứ diện bằng nhau.

 Tải ngay
Tải ngay