Tải ngay
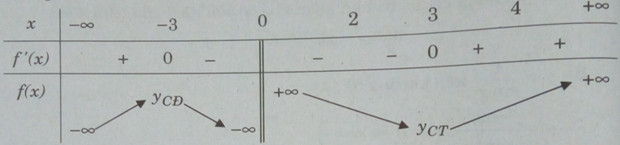
Bài 1.23 trang 20 Sách bài tập (SBT) Giải tích 12Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [2; 4] Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x) = x + {9 \over x}\) trên đoạn [2; 4] (Đề thi tốt nghiệp THPT năm 2008) Hướng dẫn làm bài: TXĐ: D = R\{0} \(\eqalign{ Hàm số nghịch biến trong các khoảng (-3; 0), (0; 3) và đồng biến trong các khoảng \(( - \infty ;3),(3; + \infty )\) Bảng biến thiên:
Ta có: \({\rm{[}}2;4] \subset (0; + \infty );f(2) = 6,5;f(3) = 6;f(4) = 6,25\) Suy ra : \(\mathop {\min }\limits_{{\rm{[}}2;4]} f(x) = f(3) = 6;\mathop {\max }\limits_{{\rm{[}}2;4]} f(x) = f(2) = 6,5\). Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
|
-
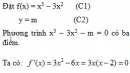
Bài 1.24 trang 20 Sách bài tập (SBT) Giải tích 12
Tìm các giá trị của m để phương trình : x3 – 3x2 – m = 0 có ba nghiệm phân biệt.
-
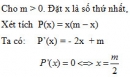
Bài 1.25 trang 20 Sách bài tập (SBT) Giải tích 12
Cho số dương m. Hãy phân tích m thành tổng của hai số dương sao cho tích của chúng là lớn nhất.
-
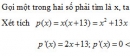
Bài 1.26 trang 20 Sách bài tập (SBT) Giải tích 12
Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất.
-
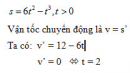
Bài 1.27 trang 20 Sách bài tập (SBT) Giải tích 12
Một chất điểm chuyển động theo quy luật s = 6t2 – t3 . Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất.
