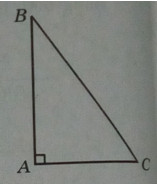
Bài 1.28 trang 20 Sách bài tập (SBT) Giải tích 12Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a > 0). Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a > 0). Hướng dẫn làm bài:
Kí hiệu cạnh góc vuông AB là x, \(0 < x < {a \over 2}\) Khi đó, cạnh huyền BC = a – x , cạnh góc vuông kia là: \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{(a - x)}^2} - {x^2}} \) Hay \(AC = \sqrt {{a^2} - 2ax} \) Diện tích tam giác ABC là: \(\eqalign{ Bảng biến thiên: Tam giác có diện tích lớn nhất khi \(AB = {a \over 3};BC = {{2a} \over 3}\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
|
-
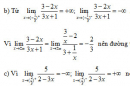
Bài 1.29 trang 22 Sách bài tập (SBT) Giải tích 12
Tìm các tiệm cận đường và ngang của đồ thị mỗi hàm số sau:
-
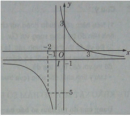
Bài 1.31 trang 23 Sách bài tập (SBT) Giải tích 12
Chỉ ra một phép biến hình biến (H) thành (H’) có tiệm cận ngang y = 2 và tiệm cận đứng x = 2.

 Tải ngay
Tải ngay