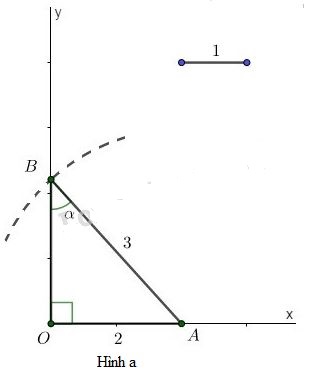
Bài 13, 14, 15, 16, 17 trang 77 SGK Toán 9 tập 1 - Luyện tập

Bài 13 trang 77 SGK Toán lớp 9 tập 1

Câu hỏi:

Dựng góc nhọn \(\alpha\) , biết:

a) \(\sin\alpha =\dfrac{2}{3}\)

b) \(\cos\alpha =0,6\)

c) \(\tan \alpha =\dfrac{3}{4}\)

d) \(\cot \alpha =\dfrac{3}{2}\) 

Lời giải: 

a) 

Ta thực hiện các bước sau:

- Dựng góc vuông \(xOy\). Lấy một đoạn thẳng làm đơn vị.

- Trên tia \(Ox\) lấy điểm \(A\) bất kỳ sao cho: \(OA=2\).

- Dùng compa dựng cung tròn tâm \(A\), bán kính \(3\). Cung tròn này cắt \(Oy\) tại điểm \(B\).

- Nối \(A\) với \(B\). Góc \(OBA\) là góc cần dựng.

Thật vậy, xét \(\Delta{OAB}\) vuông tại \(O\),  theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

          \(\sin \alpha = \sin \widehat{OBA} = \dfrac{OA}{AB}=\dfrac{2}{3}\).

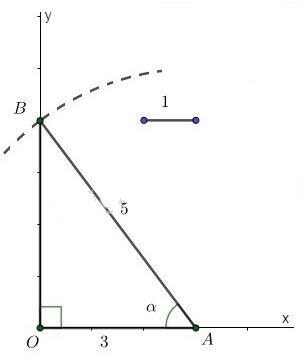
b) 

Ta có:   \(\cos \alpha =0,6 = \dfrac{3}{5}\)

 - Dựng góc vuông \(xOy\). Lấy một đoạn thẳng làm đơn vị.

- Trên tia \(Ox\) lấy điểm \(A\) bất kỳ sao cho \(OA=3\).

- Dùng compa dựng cung tròn tâm \(A\) bán kính \(5\). Cung tròn này cắt tia \(Oy\) tại \(B\).

- Nối \(A\) với \(B\). Góc \(\widehat{OAB}=\alpha \) là góc cần dựng.

Thật vậy, Xét \(\Delta{OAB}\) vuông tại \(O\), theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

           \(\cos \alpha =\cos \widehat{OAB}=\dfrac{OA}{AB}=\dfrac{3}{5}=0,6\).

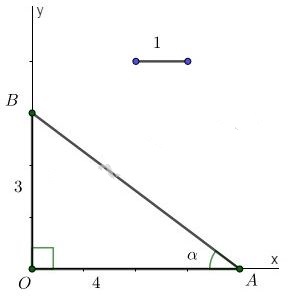
c) 

- Dựng góc vuông \(xOy\). Lấy một đoạn thẳng làm đơn vị.

- Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA=4\).

   Trên tia \(Oy\) lấy điểm \(B\) sao cho \(OB=3\).

- Nối \(A\) với \(B\). Góc \(\widehat{OAB}\) là góc cần dựng. 

Thật vậy, xét \(\Delta{OAB}\) vuông tại \(O\), theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

          \(\tan \alpha =\tan \widehat{OAB}=\dfrac{OB}{OA}=\dfrac{3}{4}.\)

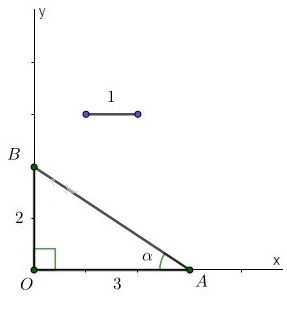
d) 

- Dựng góc vuông \(xOy\). Lấy một đoạn thẳng làm đơn vị.

- Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA=3\). 

   Trên tia \(Oy\) lấy điểm \(B\) sao cho \(OB=2\).

- Nối \(A\) với \(B\). Góc \(\widehat{OAB}\) là góc cần dựng.

Thật vậy, xét \(\Delta{OAB}\) vuông tại \(O\), theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

          \(\cot \alpha =\cot \widehat{OAB}=\dfrac{OA}{OB}=\dfrac{3}{2}.\)

Bài 14 trang 77 SGK Toán lớp 9 tập 1

Câu hỏi:

Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn \(\alpha\) tùy ý, ta có:

a) \(\tan \alpha =\dfrac{\sin\alpha }{\cos \alpha};\)   \(\cot \alpha =\dfrac{\cos \alpha }{\sin \alpha };\)         \(\tan \alpha . \cot \alpha =1\); 

b) \(\sin^{2} \alpha +\cos^{2} \alpha =1\) 

Gợi ý: Sử dụng định lý Py-ta-go.

Lời giải:

Xét \(\Delta{ABC}\) vuông tại \(A\), có \(\widehat{ACB}=\alpha\).

+) \(\Delta{ABC}\), vuông tại \(A\), theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

               \(\sin \alpha = \dfrac{AB}{BC}\),  \(\cos \alpha =\dfrac{AC}{BC}\)

              \(\tan \alpha =\dfrac{AB}{AC}\),    \(\cot \alpha =\dfrac{AC}{AB}\).

* Chứng minh \(\tan \alpha = \dfrac{\sin \alpha}{\cos \alpha}\).

   \(VP=\dfrac{\sin \alpha}{\cos \alpha}=\dfrac{AB}{BC} : \dfrac{AC}{BC}=\dfrac{AB}{BC}.\dfrac{BC}{AC}=\dfrac{AB}{AC}= \tan \alpha =VT\)

(Trong đó VT là vế trái của đẳng thức; VP là vế phải của đẳng thức)

* Chứng minh \( \cot \alpha =\dfrac{\cos \alpha}{\sin \alpha}\). 

   \(VP=\dfrac{\cos \alpha}{\sin \alpha}=\dfrac{AC}{BC} : \dfrac{AB}{BC}=\dfrac{AC}{BC}. \dfrac{BC}{AB}=\dfrac{AC}{AB}=\cot \alpha=VT\)

* Chứng minh \(\tan \alpha . \cot \alpha =1\).

Ta có: \(VT=\tan \alpha . \cot \alpha \)

                   \(= \dfrac{AB}{AC}.\dfrac{AC}{AB}=1=VP\)

b) \(\Delta{ABC}\) vuông tại \(A\), áp dụng định lí Pytago, ta được:

\(BC^2=AC^2+AB^2\)   (1)

Xét \(\sin ^{2} \alpha +\cos^{2}\alpha \)

\(\;\;\;={\left(\dfrac{AB}{BC} \right)^2}+ {\left(\dfrac{AC}{BC} \right)^2}= \dfrac{AB^{2}}{BC^{2}}+\dfrac{AC^{2}}{BC^{2}} = {{B{C^2}} \over {B{C^2}}} = 1 \) 

Như vậy \(\sin^{2} \alpha +\cos^{2} \alpha =1\) (điều phải chứng minh) 

Nhận xét: Ba hệ thức:

\(\tan \alpha =\dfrac{\sin \alpha }{\cos \alpha }\);  \(\cot \alpha =\dfrac{\cos \alpha }{\sin \alpha }\) và  \(\sin^{2} \alpha +\cos^{2}  \alpha =1\) là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.

Bài 15 trang 77 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho tam giác ABC vuông tại A. Biết cos B = 0,8, hãy tính các tỉ số lượng giác của góc C.

Gợi ý: Sử dụng bài tập 14.

Lời giải:

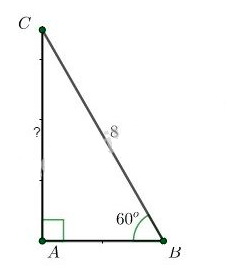
Xét tam giác \(ABC\) vuông tại \(A\) nên góc \(C\) nhọn. Vì thế:

\(\sin C>0\);  \(\cos C>0\);  \(\tan C>0\);  \(\cot C>0\).

Vì hai góc \(B\) và \(C\) phụ nhau \(\Rightarrow \sin C = \cos B = 0,8\).

Áp dụng công thức bài 14, ta có:

 \(\sin^{2}C+\cos^{2}C=1\) \(\Leftrightarrow \cos^{2}C=1-\sin^{2}C\)

                                    \(\Leftrightarrow \cos^2 C =1-(0,8)^{2}\)

                                    \(\Leftrightarrow \cos^2 C =0,36\)

                                    \(\Rightarrow \cos C = \sqrt{0,36}=0,6\)

Lại có:

\(\tan C=\dfrac{\sin C}{\cos C}=\dfrac{0,8}{0,6}=\dfrac{4}{3};\)

\(\tan C .\cot C=1 \Leftrightarrow \cot C= \dfrac{1}{\tan C}=\dfrac{3}{4}\).

Nhận xét: Nếu biết  \(\sin \alpha\) (hay \(\cos \alpha\)) thì ta có thể tính được ba tỷ số lượng giác còn lại.

Bài 16 trang 77 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho tam giác vuông có một góc bằng \(60^{\circ}\) và cạnh huyền có độ dài bằng \(8\). Hãy tìm độ dài của cạnh đối diện góc \(60^{\circ}\).

Phương pháp: 

Dựa vào định nghĩa tỷ số lượng giác của góc nhọn:

\(\sin \alpha =\dfrac{cạnh\ đối}{cạnh \ huyền} \)

\(\Rightarrow {cạnh\ đối} = \sin \alpha. {cạnh\ huyền}.\)

Lời giải:

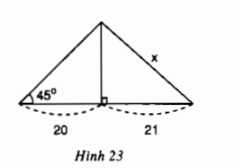
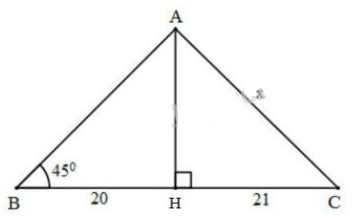
Xét \(\Delta{ABC}\) vuông tại \(A\) có \(\widehat B=60^0\), theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

\(\sin B = \dfrac{AC}{BC} \Leftrightarrow \sin 60^o = \dfrac{AC}{8}\)

\(\Leftrightarrow AC =8. \sin 60^o=8.\dfrac{\sqrt 3}{2}=4\sqrt 3.\)

Vậy cạnh đối diện với góc \(60^o\)  là \(AC=4\sqrt 3\).

Bài 17 trang 77 SGK Toán lớp 9 tập 1

Câu hỏi:

Tìm giá trị của \(x\) trong hình \(23\):

Phương pháp:

 +) Sử dụng tỷ số lượng giác: \(\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề} \Rightarrow {cạnh\ đối}=\tan \alpha . {cạnh\ kề}\). 

+) Dùng định lí Pytago trong tam giác vuông biết hai cạnh góc vuông, tính được cạnh huyền.

Lời giải:

Vẽ lại hình và đặt tên các góc như hình sau: 

Xét tam giác \(BHA\) vuông tại \(H\) có \( \widehat{B} = 45^o\), \(BH=20\) nên:

\(\tan B=\dfrac{AH}{BH} \Leftrightarrow \tan 45^o =\dfrac{AH}{20}\)

\(\Leftrightarrow AH=20. \tan 45^o = 20\)

Áp dụng định lí Pytago vào tam giác \(AHC\) vuông tại \(H\), ta có:

\(AC=\sqrt{AH^2+HC^2}=\sqrt{20^2+21^2}=29\)

Vậy \(x=29\)

Sachbaitap.com