Bài 13 trang 172 Sách bài tập (SBT) Đại số và giải tích 11Chứng minh rằng phương trình : a) \({x^5} - 5x - 1 = 0\) có ít nhất ba nghiệm ; b) \(m{\left( {x - 1} \right)^3}\left( {{x^2} - 4} \right) + {x^4} - 3 = 0\) luôn có ít nhất hai nghiệm với mọi giá trị của tham số m ; c) \({x^3} - 3x = m\) có ít nhất hai nghiệm với mọi giá trị của $m \in \left( { - 2;2} \right)\) Giải : Hướng dẫn : a) Xét hàm số \(f\left( x \right) = {x^5} - 5x - 1\) trên các đoạn \(\left[ { - 2; - 1} \right],\left[ { - 1;0} \right],\left[ {0;3} \right]\) b) Xét hàm số \(f\left( x \right) = m{\left( {x - 1} \right)^3}\left( {{x^2} - 4} \right) + {x^4} - 3\) trên các đoạn \(\left[ { - 2;1} \right],\left[ {1;2} \right]\) c) Xét hàm số \(f\left( x \right) = {x^3} - 3x - m\) trên các đoạn \(\left[ { - 1;1} \right],\left[ {1;2} \right]\)
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Ôn tập chương IV - Giới hạn - SBT Toán 11
|
-
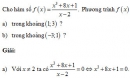
Bài 14 trang 172 Sách bài tập (SBT) Đại số và giải tích 11
Phương trình f(x) = 0 có nghiệm hay không?
-
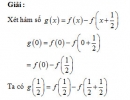
Bài 15 trang 172 Sách bài tập (SBT) Đại số và giải tích 11
Chứng minh rằng phương trình luôn có nghiệm
-

Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25 trang 173 Sách bài tập (SBT) Đại số và giải tích 11
Bài tập trắc nghiệm. Chọn đáp án đung

 Tải ngay
Tải ngay







