Tải ngay
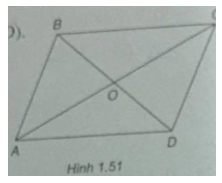
Bài 1.31 trang 34 Sách bài tập (SBT) Toán Hình học 10Cho hình bình hành ABCD có O là giao điểm của hai đường chéo Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng với điểm M bất kì ta có \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \) Gợi ý làm bài (h.1.51)
\(\overrightarrow {MA} + \overrightarrow {MC} = 2\overrightarrow {MO} \) ( Vì O là trung điểm của AC) \(\overrightarrow {MB} + \overrightarrow {MD} = 2\overrightarrow {MO} \) ( Vì O là trung điểm của BD) Vậy \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \) Sachbaitap.net
Xem lời giải SGK - Toán 10 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 3: Tích của vec tơ với một số
|
-
Bài 1.35 trang 34 Sách bài tập (SBT) Toán Hình học 10
Cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác, D là điểm đối xứng của A qua O.
