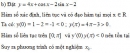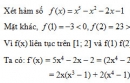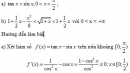Bài 1.4 Trang 8 Sách bài tập (SBT) Giải tích 12

Xét sự đồng biến, nghịch biến của các hàm số:

a) $y = x - {\mathop{\rm s}\nolimits} {\rm{inx}}$,   x ∈ [0; 2π].

b) $y = x + 2\cos x$ , x ∈ $({\pi  \over 6};{{5\pi } \over 6})$

c) $y = \sin {1 \over x}$ , (x > 0)

Hướng dẫn làm bài

a) $y = x - {\mathop{\rm s}\nolimits} {\rm{inx}}$,   x ∈ [0; 2π].

   $y' = 1 - c{\rm{osx }}$ ≥ 0 với mọi x ∈ [0; 2π]

  Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.

Vậy hàm số đồng biến trên đoạn [0; 2π].

b) $y = x + 2\cos x$ , x ∈ $({\pi  \over 6};{{5\pi } \over 6})$

    $y' = 1 - 2\sin x$ < 0  với  x ∈ $({\pi  \over 6};{{5\pi } \over 6})$

 Do đó, hàm số nghịch biến trên khoảng  $({\pi  \over 6};{{5\pi } \over 6})$

c) Xét hàm số $y = \sin {1 \over x}$  với x > 0.

                      $y' =  - {1 \over {{x^2}}}\cos {1 \over x}$

Giải bất phương trình sau trên khoảng (0; +∞):

           ${1 \over {{x^2}}}( - \cos {1 \over x}) > 0$  ⟺ $\cos {1 \over x}$ < 0

⟺ ${\pi  \over 2}(1 + 4k) < {1 \over x} < {\pi  \over 2}(3 + 4k)$ ,k = 0, 1, 2 ….

⟺ ${2 \over {\pi (1 + 4k)}} > x > {2 \over {\pi (3 + 4k)}}$  , k = 0, 1, 2 ……..

Do đó, hàm số đồng biến trên các khoảng

$....,({2 \over {(4k + 3)\pi }};{2 \over {(4k + 1)\pi }}),({2 \over {(4k - 1)\pi }};{2 \over {(4k - 3)\pi }}),.....,$ $({2 \over {7\pi }};{2 \over {5\pi }}),({2 \over {3\pi }};{2 \over \pi })$

Và nghịch biến trên các khoảng

……, $({2 \over {(4k + 1)\pi }};{2 \over {(4k - 1)\pi }}),({2 \over {5\pi }};{2 \over {3\pi }}),.....,({2 \over \pi }; + \infty )$

 với k = 0, 1, 2 …

Sachbaitap.com