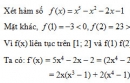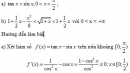Bài 1.6 trang 8 Sách bài tập (SBT) Giải tích 12Chứng minh các phương trình sau có nghiệm duy nhất Chứng minh các phương trình sau có nghiệm duy nhất a) \(3(c{\rm{os x - 1) + }}{\rm{2sin x + 6x = 0}}\) b) \(4x + c{\rm{os x - 2sin x - 2 = 0}}\) c) \( - {x^3} + {x^2} - 3x + 2 = 0$\) d) \({x^5} + {x^3} - 7 = 0\) Hướng dẫn làm bài a) Đặt y = 3(cos x – 1) + 2sin x + 6 Hàm số xác định, liên tục và có đạo hàm tại mọi x ∈ R Ta có: y( ) = 0 và ý = -3sin x + 2cos x + 6 >0, x ∈ R. Hàm số đồng biến trên R và có một nghiệm \(x = \pi \) Vậy phương trình đã cho có một nghiệm duy nhất. b) Đặt \(y = 4x + \cos x - 2\sin x - 2\) Hàm số xác định, liên tục và có đạo hàm tại mọi x ∈ R Ta có: y(0) = 1 – 2 = -1 < 0 ; \(y(\pi ) = 4\pi - 3 > 0\) . Hàm số liên tục trên \({\rm{[}}0;\pi {\rm{]}}\) và y’(0) < 0 nên tồn tại \({x_0} \in (0;\pi )\) sao cho \(y({x_0}) = 0\) . Suy ra phương trình có một nghiệm \({x_0}\) . c) Đặt y = – x3 + x2 – 3x + 2 Hàm số xác định, liên tục và có đạo hàm trên R. Ta có: y’ = – x2 + 2x – 3 < 0, \(y(\pi ) = 4\pi - 3 > 0\), x ∈ R. Vì a = -3 < 0 và . Suy ra y nghịch biến trên R. Mặt khác y(-1) = 1 + 1 +3 + 2 = 7 > 0 y(1) = -1 +1 – 3 + 2 = -1 < 0 Hàm số liên tục trên [-1; 1] và y(-1)y(1) < 0 cho nên tồn tại \({x_0} \in {\rm{[}} - 1;1]\) sao cho \(y({x_0}) = 0\) . Suy ra phương trình đã cho có đúng một nghiệm. d) Đặt y = x5 + x3 – 7 Hàm số xác định, liên tục và có đạo hàm trên R. Ta có: y(0) = -7 < 0 ; y(2) = 32 + 8 – 7 = 33 > 0 Hàm số liên tục trên [0; 2] và y(0) y(2) < 0 cho nên tồn tại \({x_0} \in (0;2)\) sao cho \(y({x_0}) = 0\) Mặt khác \(y' = 5{x^4} + 3{x^2} = {x^2}(5{x^2} + 3) \ge 0,\forall x \in R\) => Hàm số đồng biến trên \(( - \infty ; + \infty )\). Suy ra phương trình đã cho có đúng một nghiệm. Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 1. Sự đồng biến, nghịch biến của hàm số
|
-
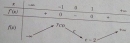
Bài 1.9 trang 9 Sách bài tập (SBT) Giải tích 12
Chứng minh rằng phương trình sau không thể có hai nghiệm thực trong đoạn [0; 1].
-

Bài 1.10 trang 9 Sách bài tập (SBT) Giải tích 12
Xác định giá trị của b để hàm số sau nghịch biến trên toàn trục số

 Tải ngay
Tải ngay