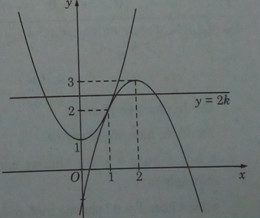
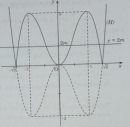
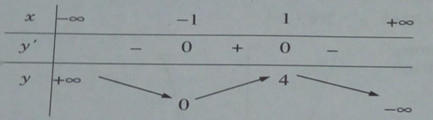Bài 1.40 trang 34 Sách bài tập (SBT) Giải tích 12Biện luận theo k số nghiệm của phương trình: Biện luận theo k số nghiệm của phương trình: a) \({(x - 1)^2} = 2|x - k|\) b) \({(x + 1)^2}(2 - x) = k\) Hướng dẫn làm bài: a) Phương trình đã cho tương đương với phương trình: \(2(x - k) = \pm {(x - 1)^2}\) \( \Leftrightarrow \left[ {\matrix{{ - {x^2} + 4x - 1 = 2k} \cr {{x^2} + 1 = 2k} \cr} } \right.\) Ta vẽ đồ thị của hai hàm số: \(y = - {x^2} + 4x - 1\) và \(y = {x^2} + 1\) Từ đồ thị ta suy ra: 2k > 3 : phương trình có hai nghiệm; 2k = 3 : phương trình có ba nghiệm; 2 < 2k < 3 : phương trình có bốn nghiệm; 2k = 2 : phương trình có ba nghiệm; 1 < 2k < 2 : phương trình có bốn nghiệm ; 2k = 1 : phương trình có ba nghiệm ; 2k < 1 : phương trình có hai nghiệm. \(\Leftrightarrow \left[ {\matrix{ (1) : phương trình có bốn nghiệm; (2): phương trình có ba nghiệm ; (3): phương trình có hai nghiệm. b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = {(x + 1)^2}(2 - x)\) . \(y = - {x^3} + 3x + 2 \Rightarrow y' = - 3{x^2} + 3\) \(y' = 0 \Leftrightarrow \left[ {\matrix{ Bảng biến thiên:
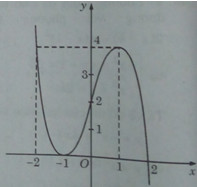
Đồ thị: Từ đồ thị hàm số ta suy ra: * k > 4 hoặc k < 0: phương trình có một nghiệm; * k = 4 hoặc k = 0 : phương trình có hai nghiệm; * 0 < k < 4: phương trình có ba nghiệm. Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
|
-
Bài 1.41 trang 34 Sách bài tập (SBT) Giải tích 12
Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m
-
Bài 1.42 trang 35 Sách bài tập (SBT) Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1)
-

Bài 1.43 trang 35 Sách bài tập (SBT) Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
-

Bài 1.44 trang 35 Sách bài tập (SBT) Giải tích 12
Xác định m để đồ thị (Cm) của hàm số đã cho có ba điểm cực trị

 Tải ngay
Tải ngay