Tải ngay
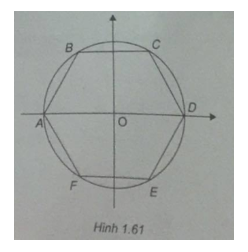
Bài 1.47 trang 44 Sách bài tập (SBT) Toán Hình học 10Cho lục giác ABCDEF Cho lục giác ABCDEF. Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\), trong đó O là tâm của lục giác đều, hai véc tơ \(\overrightarrow i \) và \(\overrightarrow {OD} \) cùng hướng, \(\overrightarrow j \) và \(\overrightarrow {EC} \) cùng hướng . Tính tọa độ các đỉnh của lục giác biết độ dài của lục giác là 6. Gợi ý làm bài (h.161)
Do ABCDEF là lục giác đều nên \(AD = 2BC = 12 \Rightarrow AO = OD = 6\) \( \Rightarrow A( - 6;0),D(6;0)\) Gọi C' là hình chiếu của C trên Ox \(\eqalign{ \( \Rightarrow C(3;3\sqrt 3 )\) B đối xứng với C qua Oy nên \(B( - 3;3\sqrt 3 )\) E đối xứng với C qua Ox nên \(E(3; - 3\sqrt 3 )\) F đối xứng với C qua O nên \(F( - 3; - 3\sqrt 3 )\) Sachbaitap.net
Xem lời giải SGK - Toán 10 - Xem ngay >> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 4: Hệ trục tọa độ
|
-
Bài 1.48 trang 45 Sách bài tập (SBT) Toán Hình học 10
Cho hình bình hành ABCD tâm O. Gọi M và N lần lượt là trung điểm của AD và BC. Dựa vào các điểm A, B, C, D, O, M, N đã cho, hãy
-
Bài 1.49 trang 45 Sách bài tập (SBT) Toán Hình học 10
Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của hai cạnh AB và CD. Nối AF và CE, hai đường thẳng này cắt đường chéo BD lần lượt tại M và N.
-
Bài 1.50 trang 45 Sách bài tập (SBT) Toán Hình học 10
Cho hai hình bình hành ABCD và ABEF với A, D, F không thẳng hàng
