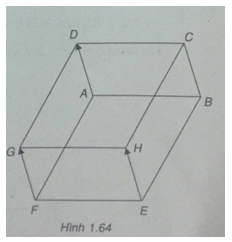
Bài 1.50 trang 45 Sách bài tập (SBT) Toán Hình học 10

Bình chọn:

4 trên 2 phiếu

Cho hai hình bình hành ABCD và ABEF với A, D, F không thẳng hàng

Cho hai hình bình hành ABCD và ABEF với A, D, F không thẳng hàng. Dựng các vec tơ $$\overrightarrow {EH} $ và $\overrightarrow {FG} $ bằng vec tơ $\overrightarrow {AD} $. Chứng minh tứ giác CDGH là hình bình hành.

Gợi ý làm bài

(h.1.64)

$\overrightarrow {EH} = \overrightarrow {AD} ,\overrightarrow {FG} = \overrightarrow {AD} = > \overrightarrow {EH} = \overrightarrow {FG} $

=>Tứ giác FEHG là hình bình hành

$ = > \overrightarrow {GH} = \overrightarrow {FE} \,(1)$

Ta có: $\overrightarrow {DC} = \overrightarrow {AB} ,\overrightarrow {AB} = \overrightarrow {FE} $

$\overrightarrow { = > DC} = \overrightarrow {FE} \,(2)$

Từ (1) và (2) ta có $\overrightarrow {GH} = \overrightarrow {DC} $

Vậy tứ giác GHCD là hình bình hành.

Sachbaitap.net

Báo lỗi - Góp ý

Xem lời giải SGK - Toán 10 - Xem ngay

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10