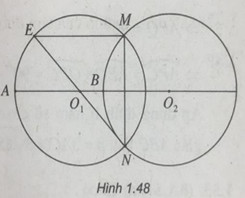
Bài 1.50 trang 41 Sách bài tập (SBT) Hình học 11Cho hai đường tròn có cùng bán kính R cắt nhau tại hai điểm M, N. Cho hai đường tròn có cùng bán kính R cắt nhau tại hai điểm M, N. Đường trung trực của MN cắt hai đường tròn tại hai điểm A, Bvà nằm cùng phía đối với MN. Chứng minh rằng \(M{N^2} + A{B^2} = 4{R^2}\). Giải:
\({T_{\overrightarrow {{O_2}{O_1}} }}:B \mapsto A\) \(M \mapsto E\) \( \Rightarrow \overrightarrow {BA} = \overrightarrow {ME} = \overrightarrow {{O_2}{O_1}} \) ∆NME vuông tại M (vì \(ME\parallel AB\) và \(AB \bot MN\)), do đó NE là đường kính. Từ đó ta có: \(\eqalign{ Sachbaitap.com
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Đề toán tổng hợp Chương I
|
-
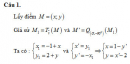
Đề 1 trang 41 Sách bài tập (SBT) Hình học 11
Viết phương trình đường thẳng d1 là ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến

 Tải ngay
Tải ngay