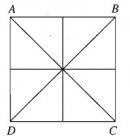
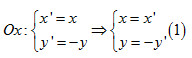Bài 1.6 trang 18 Sách bài tập (SBT) Hình học 11Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5),... Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình \(3x + 2y - 6 = 0\) và đường tròn (C) có phương trình \({x^2} + {y^2} - 2x + 4y - 4 = 0\). Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox Giải: Gọi \(M',d'\) và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox . Khi đó \(M' = \left( {3;5} \right)\) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục
Thay (1) vào phương trình của đường thẳng d ta được \(3x' - 2y' - 6 = 0\). Từ đó suy ra phương trình của d' là \(3x - 2y - 6 = 0\) Thay (1) vào phương trình của (C) ta được \(x{'^2} + y{'^2} - 2{\rm{x}}' + 4y' - 4 = 0\) . Từ đó suy ra phương trình của (C') là \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\) Cũng có thể nhận xét (C) có tâm là \(I\left( {1; - 2} \right)\) ,bán kính bằng 3,từ đó suy ra tâm I' của (C') có tọa độ (1; 2) và phương trình của (C') là \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\)
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 3. Phép đối xứng trục
|
-
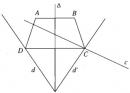
Bài 1.9 trang 18 Sách bài tập (SBT) Hình học 11
Hãy dựng điểm C trên c , điểm D trên d sao cho tứ giác ABCD là hình thang cân nhận AB là một cạnh đáy ( không cần biện luận ).
-
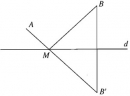
Bài 1.10 trang 18 Sách bài tập (SBT) Hình học 11
Cho đường thẳng d và hai điểm A, B không thuộc d nhưng nằm cùng phía đối với d. Tìm trên d điểm M sao cho tổng các khoảng cách từ đó đến A và B là bé nhất.

 Tải ngay
Tải ngay