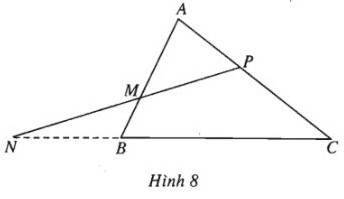
Bài 19 trang 8 SBT Hình học 10 Nâng cao

Cho tam giác \(ABC\). Các điểm \(M, N, P\) lần lượt chia các đoạn thẳng \(AB, BC, CA\) theo các tỉ số lần lượt là \(m, n, p\) (đều khác 1). Chứng minh rằng

a) \(M, N, P\) thẳng hàng khi và chỉ khi \(mnp=1\) (Định lí Mê-nê-la-uýt);

b) \(AN, CM, BP\) đồng quy hoặc song song khi và chỉ khi \(mnp=-1\) (Định lí Xê-va).

Giải

a) Lấy một điểm \(O\) nào đó ta có

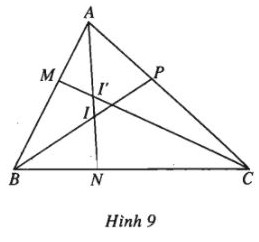
\(\eqalign{  & \overrightarrow {OM}  = {{\overrightarrow {OA}  - m\overrightarrow {OB} } \over {1 - m}}  \cr  & \overrightarrow {ON}  = {{\overrightarrow {OB}  - n\overrightarrow {OC} } \over {1 - n}}  \cr  & \overrightarrow {OP}  = {{\overrightarrow {OC}  - p\overrightarrow {OA} } \over {1 - p}} \cr} \)

Để đơn giản tính toán, ta chọn điểm O trùng với điểm C.

Khi đó ta có

\(\overrightarrow {CM}  = \dfrac{{\overrightarrow {CA}  - m\overrightarrow {CB} }}{{1 - m}};\) \(\overrightarrow {CN}  = \dfrac{{\overrightarrow {CB} }}{{1 - n}};\) \(\overrightarrow {CP}  = \dfrac{{ - p\overrightarrow {CA} }}{{1 - p}}\)                   (1)

Từ hai đẳng thức cuối của (1), ta có:

\(\overrightarrow {CB}  = (1 - n)\overrightarrow {CN} \,,\,\,\,\overrightarrow {CA}  = \dfrac{{p - 1}}{p}\overrightarrow {CP} \)

Và thay vào đẳng thức đầu của (1), ta được

\(\overrightarrow {CM}  = \dfrac{{p - 1}}{{p(1 - m)}}\overrightarrow {CP}  - \dfrac{{m(1 - n)}}{{1 - m}}\overrightarrow {CN} \)

Từ bài toán 15b) ta suy ra điều kiện cần và đủ để ba điểm \(M, N, P\) thẳng hàng là

\(\dfrac{{p - 1}}{{p(1 - m)}} - \dfrac{{m(1 - n)}}{{1 - m}} = 1\)

\(\Leftrightarrow \,\,p - 1 - pm(1 - n) = p(1 - m)\)

\(\Leftrightarrow \,\,mnp = 1.\)

b) (h.9).

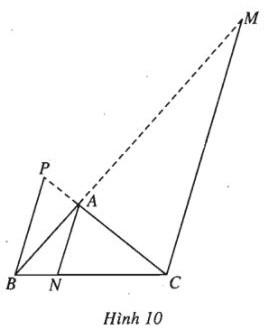
Giả sử \(AN\) cắt \(BP\) tại \(I\) và giả sử \(I\) chia đoạn thẳng \(AN\) theo tỉ số \(x\). Như vậy ba điểm \(P, I, B\) thẳng hàng và lần lượt nằm trên ba cạnh của tam giác \(CAN\). Ta có \(P\) chia đoạn thẳng \(CA\) theo tỉ số \(p, I\) chia đoạn thẳng \(AN\) theo tỉ số \(x, B\) chia đoạn thẳng \(NC\) theo tỉ số \(\dfrac{n}{{n - 1}}\) suy ra từ giả thiết \(N\) chia đoạn \(BC\) theo tỉ số \(n\)). Vậy theo định lí Mê-nê-la-uýt ta có \(p.x.\dfrac{n}{{n - 1}} = 1\,\, \Leftrightarrow \,\,x = \dfrac{{n - 1}}{{np}}\).

Giả sử \(AN\) cắt \(CM\) tại \(I’\) và \(I’\) chia \(AN\) theo tỉ số \(x’\). Như vậy ba điểm \(I’, C, M\) thẳng hàng và lần lượt nằm trên ba cạnh của tam giác \(ANB\). Ta có \(I’\) chia đoạn \(AN\) theo tỉ số \(x’, C\) chia đoạn \(NB\) theo tỉ số \(\dfrac{1}{{1 - n}}\), \(M\) chia đoạn \(BA\) theo tỉ số \(\dfrac{1}{m}\). Vậy áp dụng định lí Mê-nê-la-uýt, ta có

\(x'.\dfrac{1}{{1 - n}}.\dfrac{1}{m} = 1\,\, \Leftrightarrow \,\,x' = m(1 - n).\)

Ba đường thẳng \(AN, BP, CM\) đồng quy khi và chỉ khi \(I\) trùng \(I’ \) hay \(x=x’\), có nghĩa là:

\(\dfrac{{n - 1}}{{np}} = m(1 - n)\,\, \Leftrightarrow \,\,mnp = 1\).

+) Xét trường hợp \(AN\) và \(BP\) song song (h.10).

Ta có

\(\eqalign{  & \overrightarrow {AN}  = \overrightarrow {CN}  - \overrightarrow {CA}  = {1 \over {1 - n}}\overrightarrow {CB}  - \overrightarrow {CA} \,;  \cr  & \overrightarrow {BP}  = \overrightarrow {CP}  - \overrightarrow {CB}  = {p \over {p - 1}}\overrightarrow {CA}  - \overrightarrow {CB} \,;  \cr  & \overrightarrow {CM}  = {1 \over {1 - m}}\overrightarrow {CA}  - {m \over {1 - m}}\overrightarrow {CB} . \cr} \)

Do \(AN//BP\) nên

\(\dfrac{1}{{1 - n}}:( - 1)\, =  - 1:\dfrac{p}{{p - 1}}\)

\(\Leftrightarrow \,\,\dfrac{1}{{1 - n}} = \dfrac{{p - 1}}{p}\)

\(\Leftrightarrow \,\,p = (1 - n)(p - 1)\)

\(\Leftrightarrow \,\,\,np = n - 1.\)    (*)

Khi đó điều kiện cần và đủ để AN, BP, CM song song với nhau là \(\overrightarrow {CM} \) cùng phương với \(\overrightarrow {AN} \). Vì \(\overrightarrow {CM}  = \dfrac{{\overrightarrow {CA}  - m\overrightarrow {CB} }}{{1 - m}}\) nên \(\overrightarrow {CM} \) cùng phương với \(\overrightarrow {AN} \) khi và chỉ khi 

\(\dfrac{1}{{1 - n}}:( - m) =  - 1\)

\(\Leftrightarrow \,\,m(n - 1) =  - 1.\)   (**)

Từ (*) và (**) ta suy ra \(mnp = -1\).

Sachbaitap.com