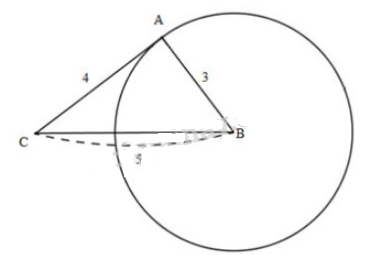
Bài 21, 22, 23 trang 111 SGK Toán 9 tập 1 - Dấu hiệu nhận biết tiếp tuyến của đường tròn

Bài 21 trang 111 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Vẽ đường tròn (B; BA). Chứng minh rằng AC là tiếp tuyến của đường tròn.

Lời giải:

Xét tam giác \(ABC\) ta có:

\(BC^2=AB^2+AC^2\) (vì \(5^2=3^2+4^2\)

Theo định lý Pytago đảo, ta có tam giác \(ABC\) vuông tại \(A\)

\(\Rightarrow\) \(AB \bot AC\) tại \(A\).

Xét đường tròn (B;BA) có đường thẳng AC đi qua điểm A thuộc đường tròn và AC vuông góc với bán kính BA nên \(AC\) là tiếp tuyến của đường tròn.

Bài 22 trang 111 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho đường thẳng \(d\), điểm \(A\) nằm trên đường thẳng \(d\), điểm \(B\) nằm ngoài đường thẳng \(d\). Hãy dựng đường tròn \((O)\) đi qua điểm \(B\) và tiếp xúc với đường thẳng \(d\) tại \(A\).

Phương pháp:

+) Bài toán dựng hình chia làm \(4\) bước:

Bước 1. Phân tích: giả sử hình cần dựng đã được vẽ. Lập luận để tìm cách dựng được hình.

Bước 2. Dựng hình: Dựa vào bước phân tích trên liệt kê thứ tự các phép dựng hình cơ bản.

Bước 3. Chứng minh: Bằng lí luận, chứng minh hình vừa dựng thỏa mãn tất cả các giả thiết của bài toán.

Bước 4. Biện luận: thiết lập điều kiện giải được của bài toán. Tức là xét xem bài toán giải được trong trường hợp nào và có bao nhiêu nghiệm.

+) Sử dụng các tính chất: Mọi điểm nằm trên đường trung trực của đoạn \(AB\) thì cách đều hai điểm \(A,\ B\)

Lời giải:

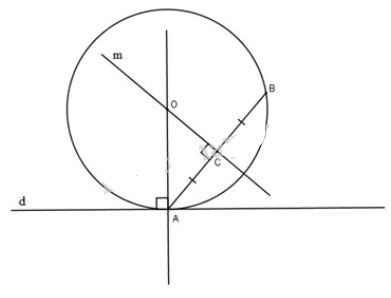
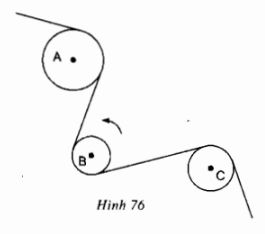
Phân tích:

Giả sử đã dựng được đường tròn thỏa mãn đề bài.

Tâm \(O\) thỏa mãn hai điều kiện:

- \(O\) nằm trên đường trung trực của \(AB\) (vì đường tròn đi qua \(A\) và \(B\)).

- \(O\) nằm trên đường thẳng vuông góc với \(d\) tại \(A\) (vì đường tròn tiếp xúc với đường thẳng \(d\) tại \(A\)).

Vậy \(O\) là giao điểm của hai đường thẳng nói trên.

Cách dựng:

- Dựng đường trung trực \(m\) của \(AB\).

- Từ \(A\) dựng một đường thẳng vuông góc với \(d\) cắt đường thẳng \(m\) tại \(O\).

- Dựng đường tròn \((O;\ OA)\). Đó là đường tròn phải dựng.

Chứng minh:

Vì \(O\) nằm trên đường trung trực của \(AB\) nên \(OA=OB\), do đó đường tròn \((O;OA)\) đi qua \(A\) và \(B\).

Đường thẳng \(d\perp OA\) tại \(A\) nên đường thẳng \(d\) tiếp xúc với đường tròn \((O)\) tại \(A\).

Biện luận: Bài toán luôn có nghiệm hình. 

Bài 23 trang 111 SGK Toán lớp 9 tập 1

Câu hỏi:

Dây cua-roa trên hình 76 có những phần là tiếp tuyến của các đường tròn tâm\(A,\ B,\ C\). Chiều quay của đường tròn tâm \(B\) ngược chiều quay của kim đồng hồ. Tìm chiều quay của đường tròn tâm \(A\) và đường tròn tâm \(C\) (cùng chiều quay hay ngược chiều quay của kim đồng hồ).

Phương pháp:

Nếu dây cua-roa mắc qua hai đường tròn mà cắt đoạn thẳng nối hai tâm đường tròn thì chiều quay của hai đường tròn sẽ ngược nhau.

Lời giải:

Ta thấy đường tròn tâm \(A\) và đường tròn tâm \(C\) cùng nằm phía dưới dây cua-roa nên sẽ quay cùng chiều nhau.

Đường tròn tâm \(B\) nằm phía trên dây cua-roa nên quay ngược chiều so với hai đường tròn tâm \(A\) và tâm \(C\).

Mà đường tròn tâm \(B\) quay ngược chiều kim đồng hồ nên đường tròn tâm \(A\) và tâm \(C\) quay cùng chiều kim đồng hồ.

Sachbaitap.com