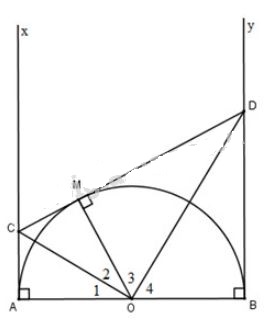
Bài 30, 31, 32 trang 116 SGK Toán 9 tập 1 - Luyện tập

Bài 30 trang 116 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho nửa đường tròn tâm \(O\) có đường kính \(AB\) (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi \(Ax,\ By\) là các tia vuông góc với \(AB\) (\(Ax,\ By\) và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ \(AB\)). Qua điểm \(M\) thuộc nửa đường tròn (\(M\) khác \(A\) và \(B\)), kẻ tiếp tuyến với nửa đường tròn, nó cắt \(Ax\) và \(By\) theo thứ tự ở \(C\) và \(D\).

Chứng minh rằng: 

a) \(\widehat {CO{\rm{D}}} = {90^0}\)

b) \(CD=AC+BD\)

c) Tích \(AC.BD\) không đổi khi điểm \(M\) di chuyển trên nửa đường tròn.

Lời giải:

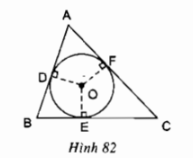
Ta có:

\(OA\perp Ax\) (gt)

\(OB\perp By\) (gt)

\(\Rightarrow\) \(Ax,\ By\) là các tiếp tuyến của đường tròn lần lượt tại \(A,\ B\).

Vì \(CA,\ CM\) là hai tiếp tuyến của \((O)\) lần lượt tại \(A\) và \(M\), theo tính chất hai tiếp tuyến cắt nhau, ta có: \(CM =CA\) và \(\widehat{O_1}=\widehat{O_2}\)

Vì \(DB,\ DM\) là hai tiếp tuyến của \((O)\) lần lượt tại \(B\) và \(M\), theo tính chất hai tiếp tuyến cắt nhau, ta có: \(DM=DB\) và \(\widehat{O_3}=\widehat{O_4}\)

a) Ta có:

\(\eqalign{
& \widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}} = {180^o} \cr
& \Leftrightarrow \left( {\widehat {{O_2}} + \widehat {{O_2}}} \right) + \left( {\widehat {{O_3}} + \widehat {{O_3}}} \right) = {180^o} \cr
& \Leftrightarrow 2\widehat {{O_2}} + 2\widehat {{O_3}} = {180^o} \cr
& \Leftrightarrow \widehat {{O_2}} + \widehat {{O_3}} = {90^o} \cr
& \Leftrightarrow \widehat {COD} = {90^o} \cr} \)

b) Ta có: \(CM=AC,\ MD=BD\) (chứng minh trên)

Lại có: \(CD=CM+MD=AC+BD\) (đpcm)

c) Ta có: \(CM=AC,\ MD=BD\) (chứng minh trên)

Xét tam giác \(COD\) vuông tại \(O\), áp dụng hệ thức lượng trong tam giác vuông, ta có:

\(MO^2=MC.MD=AC.BD=R^2\)

Vì bán kính đường tròn không đổi khi \(M\) di chuyển trên nửa đường tròn nên \(MO^2\) không đổi do đó tích \(AC.BD\) không đổi khi \(M\) di chuyển trên nửa đường tròn. 

Bài 31 trang 116 SGK Toán lớp 9 tập 1

Câu hỏi:

Trên hình \(82\), tam giác \(ABC\) ngoại tiếp đường tròn \((O)\).

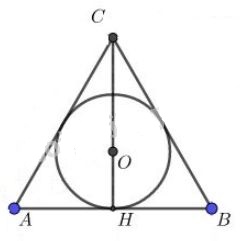
a) Chứng minh rằng:

\(2AD=AB+AC-BC.\)

b) Tìm các hệ thức tương tự hệ thức ở câu a).

Phương pháp:

+) Sử dụng tính chất hai tiếp tuyến cắt nhau để chứng minh các đoạn thẳng bằng nhau: Nếu \(AB,\ AC\) là hai tiếp tuyến của \((O)\) lần lượt tại \(A,\ B\) thì ta có: \(AB=AC\)

+) Chu vi tam giác \(ABC\) là \(C_{\Delta{ABC}}=AB+AC+BC\)

Lời giải:

a) Tam giác \(ABC\) ngoại tiếp đường tròn tâm \(O\) nên \(AB,\ BC,\ AC\) lần lượt là tiếp tuyến tại \(D,\ E,\ F\) của đường tròn.

Theo tính chất của hai tiếp tuyến cắt nhau ta có: 

\(AD=AF;\ DB=BE;\ FC=CE.\)

Xét vế phải:

\(VP=AB+AC-BC\)

\(=(AD+DB)+(AF+FC)-(BE+EC)\)

Thay \(DB=BE,\ FC=CE\) vào biểu thức trên, ta được:

\(VP=(AD+BE)+(AF+CE)-(BE+EC)\)

\(=AD+BE+AF+CE-BE-EC\)

\(=AD+AF+(BE-BE)+(CE-EC)\)

\(= AD+AF=2AD=VT.\) (Do \(AD=AF)\)

Vậy \(2AD=AB+AC-BC.\)

b) Các hệ thức tương tự là:

\(2BD=BA+BC-AC;\)

\(2CF=CA+CB-AB.\)

Nhận xét. 

Đặt \(p=\dfrac{AB+AC+BC}{2}\) là nửa chu vi của tam giác \(ABC\), \(AB=c;\ BC=a;\ CA=b\).

Ta có: \(2AD=AB+AC-BC\)

\(=(AB+AC+BC)-2BC\)

\(\Leftrightarrow AD=\dfrac{AB+AC+BC}{2}-\dfrac{2BC}{2}\)

\(\Leftrightarrow AD=p-BC\) hay \(AD=p-a\).

Tương tự ta có các kết quả sau:

\(AD=AF=p-a;\)

\(BD=BE=p-b;\)

\(CE=CF=p-c.\)

Bài 32 trang 116 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho tam giác đều \(ABC\) ngoại tiếp đường tròn bán kính \(1cm\). Diện tích của tam giác \(ABC\) bằng:

(A) \(6cm^{2}\);

(B) \(\sqrt{3}cm^{2}\);

(C) \(\dfrac{3\sqrt{3}}{4}cm^{2}\)

(D) \(3\sqrt{3}cm^{2}.\)

Hãy chọn câu trả lời đúng.

Phương pháp:

+) Sử dụng tính chất: Trong tam giác đều, đường cao đồng thời là đường trung tuyến.

+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông: \(\Delta{ABC}\) vuông tại \(A\). Khi đó: \(AB=BC. \sin C;\ AC=BC. \sin B\). 

+) Công thức tính diện tích tam giác: \(S=\dfrac{1}{2}.h.a\)

trong đó \(h\) là độ dài đường cao, \(a\) là độ dài cạnh ứng với đường cao.

Lời giải:

Gọi \((O)\) là đường tròn nội tiếp tam giác đều \(ABC\) và H là tiếp điểm thuộc AB. 

Khi đó \(OH=1\) là bán kính của \((O)\)

Ta có: \(CH\bot AB\)

Trong tam giác đều ABC, đường cao CH cũng là đường trung tuyến.

Vì tam giác ABC đều nên O cũng là trọng tâm tam giác.

Theo tính chất đường trung tuyến, ta có:

\(OH=\dfrac{1}{3}CH \Rightarrow CH=3.OH=3.1=3.\)

Vì tam giác \(ABC\) đều nên \(\widehat{B}=60^o\).

Xét tam giác \(CHB\), vuông tại \(H\), \(\widehat{B}=60^o,\ CH=3\). Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông, ta có:

\(CH=CB. \sin B \Rightarrow CB=\dfrac{CH}{\sin B}=\dfrac{3}{\sin 60^o}=2\sqrt 3\)

Suy ra \(AB=AC=BC=2\sqrt{3}(cm).\)

Do đó diện tích tam giác \(ABC\) là

\(S=\dfrac{1}{2}CH.AB=\dfrac{1}{2}.3. 2\sqrt{3}=3\sqrt{3}(cm^{2}).\) 

Ta chọn (D).

Sachbaitap.com