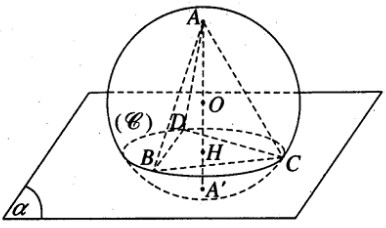
Bài 2.23 trang 64 sách bài tập (SBT) – Hình học 12Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho . Mặt phẳng qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C). Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho \(AH = {{4r} \over 3}\) . Mặt phẳng \((\alpha )\) qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C). a) Tính diện tích của hình tròn (C) . b) Gọi BCD là tam giác đều nội tiếp trong (C), hãy tính thể tích hình chóp A.BCD và hình chóp A’.BCD. Hướng dẫn làm bài: Hình 2.45 a) Theo giả thiết ta có \(AH = {{4r} \over 3}\) Ta suy ra \(OH = {r \over 3}\) . Gọi r’ là bán kính của đường tròn (C). Ta có: \(r{'^2} = {r^2} - O{H^2} = {r^2} - {{{r^2}} \over 9} = {{8{r^2}} \over 9}\) Vậy diện tích của hình tròn (C) là: \(S = \pi r{'^2} = {{8\pi {r^2}} \over 9}\) b) Vì BCD là tam giác đều nên ta có: \(BC = r'.\sqrt 3 = {{2\sqrt 6 } \over 3}r\)
Diện tích của tam giác đều BCD là \(S = {{B{C^2}\sqrt 3 } \over 4} = {{24{r^2}} \over 9}.{{\sqrt 3 } \over 4} = {{2{r^2}\sqrt 3 } \over 3}\) Thể tích hình chóp A.BCD là : \(V = {1 \over 3}{{2{r^2}\sqrt 3 } \over 3}.{{4r} \over 3} = {{8\sqrt 3 {r^3}} \over {27}}\) Hai hình chóp A.BCD và A’.BCD có chung mặt đáy BCD nên:\({{{V_{A'.BCD}}} \over {{V_{A.BCD}}}} = {{HA'} \over {HA}} = {1 \over 2}\). Do đó, \({V_{A'.BCD}} = {{4\sqrt 3 {r^3}} \over {27}}\). Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 2. Mặt cầu
|
-
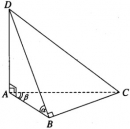
Bài 2.24 trang 65 sách bài tập (SBT) – Hình học 12
Cho tứ diện ABCD có và . Khi quay tất cả các cạnh của tứ diện đó quanh cạnh AB có những hình nón nào được tạo thành ? Hãy kể tên các hình nón đó.
-
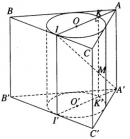
Bài 2.25 trang 65 sách bài tập (SBT) – Hình học 12
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và có đường cao h.
-
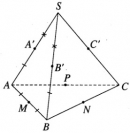
Bài 2.26 trang 65 sách bài tập (SBT) – Hình học 12
Cho hình chóp S.ABC và biết rằng có một mặt cầu tiếp xúc với tất cả các cạnh bên của hình chóp đồng thời tiếp xúc với ba cạnh của đáy tại trung điểm của mỗi cạnh đáy. Chứng minh hình chóp đó là hình chóp đều.
-
Bài 2.27 trang 65 sách bài tập (SBT) – Hình học 12
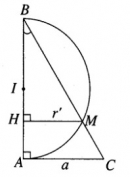
Trong mặt phẳng a, cho tam giác ABC vuông tại A có cạnh AC = a và có cạnh huyền BC = 2a. Cũng trong mặt phẳng đó cho nửa đường tròn đường kính AB cắt cạnh BC tại M.

 Tải ngay
Tải ngay