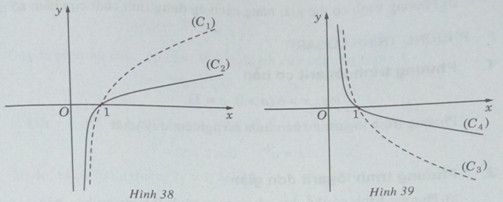
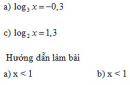Bài 2.28 trang 116 Sách bài tập (SBT) Giải tích 12Hãy chỉ rõ đồ thị tương ứng với mỗi hàm số và giải thích. Các hình 38 và 39 là đồ thị của bốn hàm số: \(y = {\log _{\sqrt 2 }}x;y = {\log _{\frac{1}{e}}}x;y = {\log _{\sqrt 5 }}x;y = {\log _{\frac{1}{3}}}\) Hãy chỉ rõ đồ thị tương ứng với mỗi hàm số và giải thích. Hướng dẫn làm bài: Ta có (C1), (C2) đi lên từ trái sang phải nên là đồ thị của các hàm số đồng biến, tức là ứng với hàm số logarit có cơ số lớn hơn 1. Mặt khác, khi x > 1 thì \({\log _{\sqrt 2 }}x > {\log _{\sqrt 5 }}x\) và khi 0 < x < 1 thì \({\log _{\sqrt 2 }}x < {\log _{\sqrt 5 }}\) Do đó, (C1) là đồ thị của hàm số \(y = {\log _{\sqrt 2 }}x\) , (C2) là đồ thị của hàm số \(y = {\log _{\sqrt 2 }}x\) Ta có (C3), (C4) đi xuống từ trái sang phải nên là đồ thị của các hàm số nghịch biến, nghĩa là ứng với hàm số logarit có cơ số nhỏ hơn 1. Mặt khác, khi x > 1 thì \({\log _{\frac{1}{e}}}x < {\log _{\frac{1}{3}}}x\) và khi 0 < x < 1 thì \({\log _{\frac{1}{e}}}x > {\log _{\frac{1}{3}}}x\) Do đó, (C3) là đồ thị của hàm số \(y = {\log _{\frac{1}{e}}}x\) ; (C4) là đồ thị của hàm số \(y = {\log _{\frac{1}{3}}}x\). Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 4. Hàm số mũ. Hàm số logarit
|
-

Bài 2.32 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình sau bằng phương pháp đồ thị:

 Tải ngay
Tải ngay