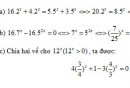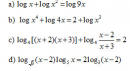Bài 2.30 trang 125 Sách bài tập (SBT) Giải tích 12Giải các phương trình mũ sau: Giải các phương trình mũ sau: a) \({(0,75)^{2x - 3}} = {(1\frac{1}{3})^{5 - x}}\) b) \({5^{{x^2} - 5x - 6}} = 1\) c) \({(\frac{1}{7})^{{x^2} - 2x - 3}} = {7^{x + 1}}\) d) \({32^{\frac{{x + 5}}{{x - 7}}}} = 0,{25.125^{\frac{{x + 17}}{{x - 3}}}}\) Hướng dẫn làm bài: a) \({(\frac{3}{4})^{2x - 3}} = {(\frac{4}{3})^{5 - x}}\) \( \Leftrightarrow {(\frac{3}{4})^{2x - 3}} = {(\frac{3}{4})^{x - 5}}\) \(\Leftrightarrow 2x - 3 = x - 5 \Leftrightarrow x = - 2\) b) \(\begin{array}{l} c) \(\begin{array}{l} d) \({2^{5.\frac{{x + 5}}{{x - 7}}}} = {2^{ - 2}}{.5^{3.\frac{{x + 17}}{{x - 3}}}} < = > {2^{\frac{{5x + 25}}{{x - 7}} + 2}} = {5^{\frac{{3x + 51}}{{x - 3}}}} < = > {2^{\frac{{7x + 11}}{{x - 7}}}} = {5^{\frac{{3x + 51}}{{x - 3}}}}\) Lấy logarit cơ số 2 cả hai vế, ta được: \(\frac{{7x + 11}}{{x - 7}} = \frac{{3x + 51}}{{x - 3}}{\log _2}5 < = > \left\{ {\begin{array}{*{20}{c}} \( < = > (7 - 3{\log _2}5){x^2} - 2(5 + 15{\log _2}5) - (33 - 357{\log _2}5) = 0\) Ta có: \(\Delta ' = {(5 + 15{\log _2}5)^2} + (7 - 3{\log _2}5)(33 - 357{\log _2}5)\) \( = 1296\log _2^25 - 2448{\log _2}5 + 256 > 0\) Phương trình đã cho có hai nghiệm: \(x = \frac{{5 + 15{{\log }_2}5 \pm \sqrt {\Delta '} }}{{7 - 3{{\log }_2}5}}\) , đều thỏa mãn điều kiện
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 5. Phương trình mũ và phương trình logarit
|
-

Bài 2.32 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình sau bằng phương pháp đồ thị:
-
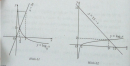
Bài 2.34 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình sau bằng phương pháp đồ thị:

 Tải ngay
Tải ngay