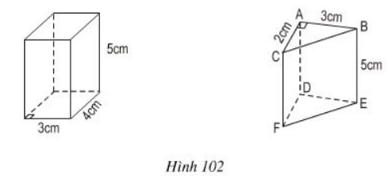
Bài 23, 24, 25, 26 trang 111, 112 SGK Toán 8 tập 2 - Diện tích xung quanh của hình lăng trụ đứng

Bài 23 trang 111 SGK Toán lớp 8 tập 2

Câu hỏi:

Tính diện tích xung quanh, diện tích toàn phần của các lăng trụ đứng sau đây (h.102):

Lời giải:

a) Với hình vẽ bên trái :

Diện tích xung quanh của lăng trụ đứng là: 

         \(2.(3+ 4) . 5 = 70 (cm^2) \)

Diện tích toàn phần của lăng trụ đứng là:

         \(70 + 2.3.4 = 94(cm^2) \)

b) Với hình vẽ bên phải: 

 \( \triangle ABC \) vuông tại  \(A \Rightarrow BC^2 = AB^2 + AC^2 = 9 + 4 = 13\)

\( \Rightarrow BC = \sqrt{13} (cm)  \)

Chu vi đáy là: \(2+3+\sqrt {13}=5+\sqrt {13}\)

Diện tích xung quanh của lăng trụ đứng là:

        \( (5+\sqrt {13}).5 = 25 + 5\sqrt{13}  (cm^2 )\)

Diện tích toàn phần của lăng trụ đứng là:

        \( 25 + 5\sqrt{13} + 2(\dfrac{1}{2}. 2.3) \)

        \(= 25 + 5\sqrt{13} + 6= 31 + 5\sqrt{13}(cm^2 ) \) 

Bài 24 trang 111 SGK Toán lớp 8 tập 2

Câu hỏi:

Quan sát lăng trụ đứng tam giác (h.103) rồi điền số thích hợp vào các ô trống ở bảng sau:

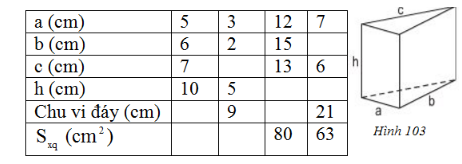
Phương pháp:

Dựa vào công thức tính diện tích xung quanh hình lăng trụ đứng: \(S_{xq} = 2p.h\) với \(p\) là nửa chu vi đáy, \(h\) là chiều cao lăng trụ.

+ Chu vi đáy \(C= a + b + c\) (kí hiệu C là chu vi đáy)

+ Diện tích xung quanh = chu vi đáy x chiều cao

Lời giải:

Chu vi đáy là: \(C=5+6+7=18 \;cm\)

\({S_{xq}} = 18.10 = 180\;cm^2\)

Cột 2:

Độ dài cạnh thứ 3 của tam giác đáy là \(c=9-3-2=4\)

\({S_{xq}} = 9.5 = 45\;cm^2\)

Cột 3:

Chu vi đáy là \(C=12+15+13=40\;cm\)

Chiều cao là: \(h = \dfrac{{{S_{xq}}}}{{C}} = \dfrac{{80}}{{40}} = 2\;cm\)

Cột 4:

Độ dài cạnh còn lại của tam giác đáy là: \(b=21-7-6=8\;cm\)

Chiều cao là: \(h = \dfrac{{{S_{xq}}}}{C} = \dfrac{{63}}{{21}} = 3\;cm\) 

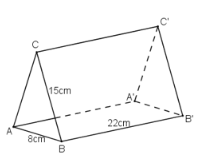
Bài 25 trang 111 SGK Toán lớp 8 tập 2

Câu hỏi:

Tấm lịch để bàn (xem lại hình 94) có dạng một lăng trụ đứng, ABC là một tam giác cân (h.104).

a) Hãy vẽ thêm nét khuất, điền thêm chữ vào các đỉnh rồi cho biết AC song song với những cạnh nào?

Phương pháp:

a. Dựa vào định nghĩa hình lăng trụ đứng. 

b.

- Diện tích miếng bìa dùng để làm tấm lịch như trên chính là diện tích xung quanh của lăng trụ đứng có đáy là một tam giác cân.

- Tính diện tích xung quanh hình lăng trụ đứng bằng tích của chu vi đáy và chiều cao. 

- Chu vi tam giác bằng tổng độ dài ba cạnh của tam giác đó.

Lời giải:

a. Cạnh \(AC\) song song với cạnh \(A’C’.\)

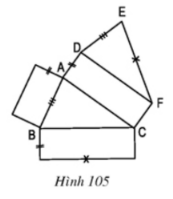
b. Diện tích miếng bìa dùng để làm tấm lịch như trên là diện tích xung quanh của lăng trụ đứng.

Tam giác \(ABC\) là tam giác cân tại C nên \(AC=BC=15cm\)

Chu vi tam giác \(ABC\) là:

\(15.2+8=38\;cm\)

Diện tích xung quanh của lăng trụ đứng như trên là:  

\( 38. 22 = 836\;(cm^2 ) \)

Vậy diện tích miếng bìa dùng để làm một tấm lịch như trên là  \(836cm^2 \).

Bài 26 trang 112 SGK Toán lớp 8 tập 2

Câu hỏi:

 a) Từ hình khai triển (h.105) có thể gấp theo các cạnh để có được một lăng trụ đứng hay không? (Các tứ giác trên hình đều là những hình chữ nhật).

b) Trong hình vừa gấp được, xét xemm các phát biểu dưới đây, phát biểu nào đúng?

- Cạnh AD vuông góc với cạnh AB.

- EF và CF là hai cạnh vuông với nhau.

- Cạnh DE và cạnh BC vuông góc với nhau.

- Hai đáy (ABC) và (DEF) nằm trên hai mặt phẳng song song với nhau.

- Mặt phẳng (ABC) song song với mặt phẳng (ACFD).

Lời giải:

a) Từ hình khai triển bên, ta có thể gấp theo các cạnh để được hình lăng trụ đứng.

b) Các phát biểu đúng:

- Cạnh \(AD\) vuông góc với cạnh \(AB\).

- \(EF\) và \(CF\) là hai cạnh vuông góc với nhau.

- Hai đáy \((ABC)\) và \((DEF)\) nằm trên hai mặt phẳng song song với nhau.

Sachbaitap.com