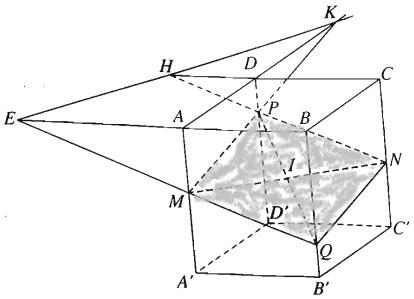
Bài 2.40 trang 84 Sách bài tập (SBT) Hình học 11Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA’ và CC’. Một điểm P nằm trên cạnh bên DD’. Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA’ và CC’. Một điểm P nằm trên cạnh bên DD’. a) Xác định giao điểm Q của đường thẳng BB’ với mặt phẳng (MNP). b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện. Thiết diện đó có tính chất gì? c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp. Giải:
a) Ta có mặt phẳng (AA’, DD’) song song với mặt phẳng (BB’, CC’). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song. Nếu gọi Q là điểm trên cạnh BB’ sao cho \(NQ\parallel PM\) thì Q là giao điểm của đường thẳng BB’ với mặt phẳng (MNP) Nhận xét. Ta có thể tìm điểm Q bằng cách nối P với trung điểm I của đoạn MN và đường thẳng PI cắt BB’ tại Q. b) Vì mặt phẳng (AA’, BB’) song song với mặt phẳng (DD’, CC’) nên ta có \(MQ\parallel PN\). Do đó mặt phẳng (MNP) cắt hình hộp theo thiết diện MNPQ là một ình bình hành. Giả sử P không phải là trung điểm của đoạn DD’. Gọi \(H = PN \cap DC,K = MP \cap A{\rm{D}}\). Ta có D = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp. Chú ý rằng giao điểm \(E = AB \cap MQ\) cũng nằm trên giao tuyến d nói trên. Khi P là trung điểm của DD’ mặt phẳng (MNP) song song với mặt phẳng (ABCD). Sachbaitap.com
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|
-
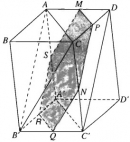
Bài 2.41 trang 85 Sách bài tập (SBT) Hình học 11
Cho hình hộp ABCD.A’B’C’D’. Hai điểm M và N lần lượt nằm trên hai cạnhAD và CC’ sao cho
-
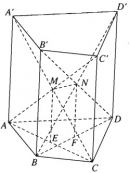
Bài 2.42 trang 85 Sách bài tập (SBT) Hình học 11
a) Chứng minh rằng hai đường chéo AC’ và A’C cắt nhau và hai đường chéo BD’ và B’Dcắt nhau.
-
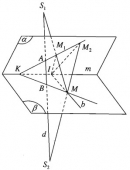
Bài 2.43 trang 85 Sách bài tập (SBT) Hình học 11
b) Giả sử đường thẳng M1M2 cắt giao tuyến m tại K. Chứng minh rằng ba điểm K, B, M thẳng hàng.
-
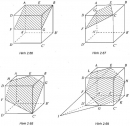
Bài 2.44 trang 85 Sách bài tập (SBT) Hình học 11
Cho hình lập phương ABCD.A’B’C’D’ các trung điểm E, F của các cạnh AB, DD’. Hãy xác định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC’) và (EFK) với K là trung điểm của cạnh B’C’.

 Tải ngay
Tải ngay