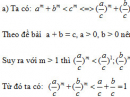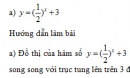Bài 2.44 trang 132 Sách bài tập (SBT) Giải tích 12Tìm tập xác định của các hàm số sau: Tìm tập xác định của các hàm số sau: a) \(y = \frac{2}{{\sqrt {{4^x} - 2} }}\) b) \(y = {\log _6}\frac{{3x + 2}}{{1 - x}}\) c) \(y = \sqrt {\log x + \log (x + 2)} $\) d) \(y = \sqrt {\log (x - 1) + \log (x + 1)} \) Hướng dẫn làm bài: a) Hàm số xác định khi: \({4^x} - 2 > 0\Leftrightarrow {2^{2x}} > 2\Leftrightarrow x > \frac{1}{2}\) Vậy tập xác định là \(D = (\frac{1}{2}; + \infty )\) b) \(D = ( - \frac{2}{3};1)\) c) \(\eqalign{& \log x + \log (x + 2) \ge 0 \cr & \Leftrightarrow \left\{ {\matrix{{\log [x(x + 2){\rm{]}} \ge \log 1} \cr {x > 0} \cr} } \right. \cr & \Leftrightarrow \left\{ {\matrix{{{x^2} + 2x - 1 \ge 0} \cr {x > 0} \cr} } \right. \cr & \Leftrightarrow \left\{ {\matrix{{\left[ {\matrix{{x \le - 1 - \sqrt 2 } \cr {x \ge - 1 + \sqrt 2 } \cr} } \right.} \cr {x > 0} \cr} } \right. \Leftrightarrow x \ge - 1 + \sqrt 2 \cr}\) Vậy tập xác định là \(D = {\rm{[}} - 1 + \sqrt 2 ; + \infty )\) d) Tương tự câu c, \(D = {\rm{[}}\sqrt 2 ; + \infty )\). Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Ôn tập Chương II - Hàm số lũy thừa. Hàm số mũ và hàm số Lôgarit
|
-
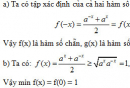
Bài 2.45 trang 133 Sách bài tập (SBT) Giải tích 12
Chứng minh rằng f(x) là hàm số chẵn, g(x) là hàm số lẻ.

 Tải ngay
Tải ngay