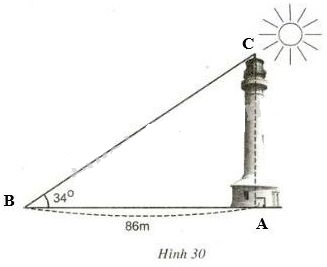
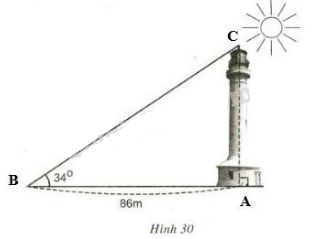
Bài 26, 27 trang 88 SGK Toán 9 tập 1 - Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 26 trang 88 SGK Toán lớp 9 tập 1

Câu hỏi:

Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng \(34^{\circ}\) và bóng của một tháp trên mặt đất dài \(86m\) (H.30). Tính chiều cao của tháp (làm tròn đến mét).

Phương pháp:

+) Tháp đặt vuông góc với mặt đất nên ta có tam giác vuông.

+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông: \(\Delta{ABC}\) vuông tại \(A\) thì:

\(AC=AB. \tan B = AB. \cot C\) 

Lời giải:

Đặt tên các điểm như hình vẽ.

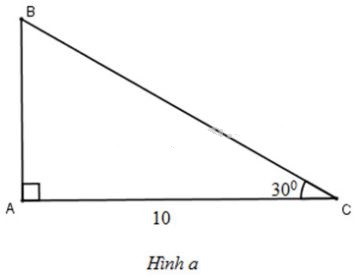
Xét tam giác \(ABC\) vuông tại \(A\), theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:

\(\tan B = \dfrac{AC}{AB} \Leftrightarrow \tan 34^o = \dfrac{AC}{86}\)

\(\Leftrightarrow AC = 86. \tan 34^o \approx 58 (m)\)

Vậy chiều cao của tháp là: \( 58 \left ( m \right )\).

Bài 27 trang 88 SGK Toán lớp 9 tập 1

Câu hỏi:

Giải tam giác \(ABC\) vuông tại \(A\), biết rằng:

a) \(b=10cm;\ \widehat{C}=30^{\circ}\)

b) \(c=10cm;\ \widehat{C}=45^{\circ}\)

c) \(a=20cm;\ \widehat{B}=35^{\circ}\)

d) \(c=21cm;\ b=18cm\)

Lời giải: 

a) 

 Quy ước: Tam giác ABC vuông tại A có a = BC ; b = AC; c = AB

(H.a)

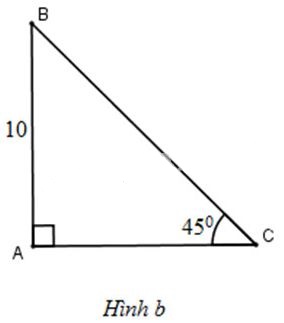
+) Ta có: \(\widehat{B} + \widehat{C}=90^{\circ} \Rightarrow \widehat{B}=90^o -30^{\circ}=60^{\circ}\)

+) Lại có 

\(AB = AC. \tan C=10.tan 30^o=\dfrac{10\sqrt 3}{3} \approx 5,77(cm)\)

\(AC=BC. \cos C \Rightarrow 10=BC. \cos 30^o \Rightarrow BC=\dfrac{10}{\cos 30^o}=\dfrac{20\sqrt 3}{3} \approx 11,55(cm)\).

b) 

(H.b)

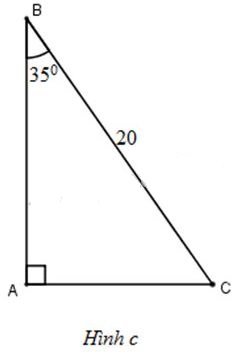
+) Xét tam giác \(ABC\) vuông tại \(A\) có \(AB=10,\ \widehat{C}=45^o\) nên \(ABC\) là tam giác vuông cân tại A \(\Rightarrow \widehat{B}=45^{\circ}; AB=AC=10(cm)\)

+) Lại có: \(AB=BC. \sin C \Rightarrow 10=BC. sin 45^o\)

\(\Rightarrow BC=\dfrac{10}{\sin 45^o}=10\sqrt 2 \approx 14,14(cm).\)

c) 

 (H.c) 

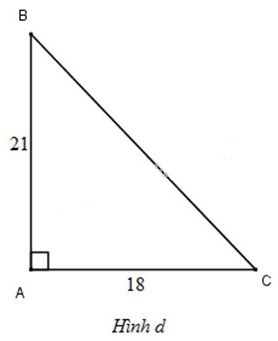
+) Ta có: \(\widehat{C}+ \widehat{B}=90^{\circ} \Rightarrow \widehat{C}= 90^o - \widehat{B}=90^o - 35^{\circ}=55^{\circ}.\) 

+) Lại có: \(AB=BC\cdot cosB=20\cdot cos35^{\circ}\approx 16,383 (cm)\)

                \(AC= BC \cdot sinB=20\cdot sin35^{\circ}\approx 11,472 (cm)\).

d) 

(H.d)

Áp dụng định lí Pytago vào tam giác vuông ABC, ta được: \(BC^2=AC^2+AB^2=18^2 +21^2=765\)

\(\Rightarrow BC = \sqrt{765}=3\sqrt{85} \approx 27,66(cm)\)

Lại có:

\(\tan B=\dfrac{AC}{AB}=\dfrac{18}{21} \approx 0,8571\)

Bấm máy tính: SHIFT tan 0,8571 \(\Rightarrow \widehat{B}\approx 41^{\circ}\)

Vì \(\widehat{C }+\widehat{B}=90^o \Rightarrow \widehat{C}= 90^o - 41^o =49^{\circ}\) 

Sachbaitap.com