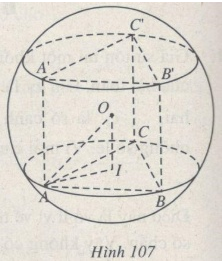
Bài 3 trang 223 Sách bài tập Hình học lớp 12 Nâng caoXét hình lăng trụ tam giác đều với chiều cao h Xét hình lăng trụ tam giác đều với chiều cao h, nội tiếp một mặt cầu bán kính R (h < 2R) (tức sáu đỉnh của hình lăng trụ nằm trên mặt cầu đó). a) Tính cạnh đáy của hình lăng trụ. b) Tính thể tích của khối lăng trụ. c) Tính h theo R để mỗi mặt bên của hình lăng trụ là hình vuông. Giải (h.107).
a) Gọi O là tâm của mặt cầu ngoại tiếp hình lăng trụ, I là hình chiếu của O trên mặt phẳng (ABC). Khi đó ta có : \(OA = OB = OC = R,OI = {1 \over 2}h.\) Tam giác OAI vuông tại I nên\(A{I^2} = O{A^2} - {\rm{ }}O{I^2} = {\rm{ }}{R^2}\; - {{{h^2}} \over 4}.\) IA là bán kính đường tròn ngoại tiếp tam giác đều ABC nên \(AB = IA\sqrt 3 = \sqrt {3\left( {{R^2} - {{{h^2}} \over 4}} \right)} .\) Vậy cạnh đáy của hình lăng trụ bằng \({1 \over 2}\sqrt {3\left( {4{R^2} - {h^2}} \right)} .\) b) Thể tích của khối lăng trụ ABC.A'B'C' là : \(V = {S_{ABC}}.h = {{A{B^2}\sqrt 3 } \over 4}h = {{3\sqrt 3 } \over {16}}\left( {4{R^2} - {h^2}} \right)h.\) c) Mỗi mặt bên của hình lăng trụ là hình vuông khi và chỉ khi AB = h, tức \({1 \over 2}\sqrt {3\left( {4{R^2} - {h^2}} \right)} = h \Leftrightarrow h = \sqrt {{{12} \over 7}} R\) (để ý rằng \(\sqrt {{{12} \over 7}} \)< 2). Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Ôn tập cuối năm Hình học
|
-
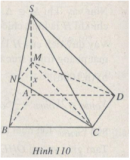
Bài 6 trang 223 Sách bài tập Hình học lớp 12 Nâng cao.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a

 Tải ngay
Tải ngay