Tải ngay
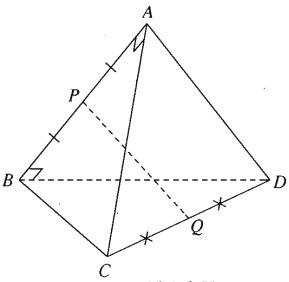
Bài 3.15 trang 141 Sách bài tập (SBT) Hình học 11Chứng minh rằng AB và PQ vuông góc với nhau. Cho tứ diện ABCD trong đó \(AB \bot AC,AB \bot B{\rm{D}}\). Gọi P và Q lần lượt là trung điểm của AB và CD. Chứng minh rằng AB và PQ vuông góc với nhau. Giải:
\(\eqalign{ Cộng từng vế (1) và (2) ta có: \(2\overrightarrow {PQ} = \overrightarrow {AC} + \overrightarrow {B{\rm{D}}} \) Suy ra \(2\overrightarrow {PQ} .\overrightarrow {AB} = \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {B{\rm{D}}} .\overrightarrow {AB} = 0\) Hay \(\overrightarrow {PQ} .\overrightarrow {AB} = 0\), tức là \(PQ \bot AB\). Sachbaitap.com
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Chú ý! Lộ Trình Sun 2027 - 1 lộ trình ôn đa kỳ thi (TN THPT, ĐGNL (Hà Nội/ Hồ Chí Minh), ĐGNL Sư Phạm, ĐGTD, ĐGNL Bộ Công an, ĐGNL Bộ Quốc phòngTD - Click xem ngay) tại Tuyensinh247.com. Cập nhật bám sát bộ SGK mới, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 2. Hai đường thẳng vuông góc
|
-
Bài 3.16 trang 147 Sách bài tập (SBT) Hình học 11
Chứng minh ba điểm A’, O, B’ thẳng hàng và AA’ = BB’
-
Bài 3.17 trang 147 Sách bài tập (SBT) Hình học 11
Chứng minh rằng hai mặt phẳng cắt nhau và giao tuyến d của chúng vuông góc với mặt phẳng (ABC)
-
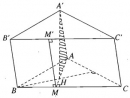
Bài 3.18 trang 147 Sách bài tập (SBT) Hình học 11
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trực tâm của tam giác ABC và biết rằng A’H vuông góc với mặt phẳng (ABC). Chứng minh rằng:
-
Bài 3.19 trang 147 Sách bài tập (SBT) Hình học 11
Hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A và có cạnh bên SA vuông góc với mặt phẳng đáy là (ABC).
