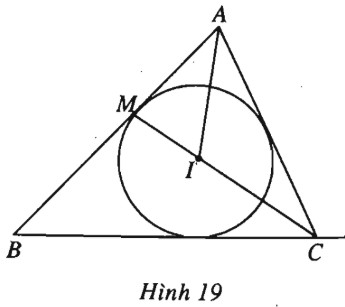
Bài 37 trang 11 SBT Hình học 10 Nâng cao

Cho tam giác \(ABC\) với các cạnh \(AB=c, BC=a, CA=b.\)

a) Gọi \(CM\) là đường phân giác trong của góc \(C\). Hãy biểu thị vec tơ \(\overrightarrow {CM} \) theo các vec tơ \(\overrightarrow {CA} \) và \(\overrightarrow {CB} \).

b) Gọi \(I\) là tâm đường tròn nội tiếp tam giác \(ABC\). Chứng minh rằng

\(a\overrightarrow {IA}  + b\overrightarrow {IB}  + c\overrightarrow {IC}  = \overrightarrow 0 \).

Giải

(h.19).

a) Theo tính chất đường phân giác , ta có

\(\dfrac{{AM}}{{BM}} = \dfrac{{CA}}{{CB}} = \dfrac{b}{a}\), suy ra \(\overrightarrow {MA}  =  - \dfrac{b}{a}\overrightarrow {MB} \).

Từ đó , ta có \(\overrightarrow {CM}  = \dfrac{{\overrightarrow {CA}  + \dfrac{b}{a}\overrightarrow {CB} }}{{1 + \dfrac{b}{a}}}\)

\(= \dfrac{a}{{a + b}}\overrightarrow {CA}  + \dfrac{b}{{a + b}}\overrightarrow {CB} .\)

b) Vì \(I\) là tâm đường tròn nội tiếp tam giác \(ABC\) nên \(AI\) là phân giác của tam giác \(ACM\). Bởi vậy theo câu a), ta có biểu thị vec tơ \(\overrightarrow {AI} \) theo hai vec tơ \(\overrightarrow {AM} \) và \(\overrightarrow {AC} \).

\(\begin{array}{l}\overrightarrow {AI}  = \dfrac{{AC}}{{AC + AM}}\overrightarrow {AM}  + \dfrac{{AM}}{{AC + AM}}\overrightarrow {AC}\\  = \dfrac{b}{{b + \dfrac{{bc}}{{a + b}}}}.\dfrac{b}{{a + b}}\overrightarrow {AB}  + \dfrac{{\dfrac{{bc}}{{a + b}}}}{{b + \dfrac{{bc}}{{a + b}}}}\overrightarrow {AC} \\ = \dfrac{b}{{a + b + c}}\overrightarrow {AB}  + \dfrac{c}{{a + b + c}}\overrightarrow {AC}\\  = \dfrac{b}{{a + b + c}}(\overrightarrow {IB}  - \overrightarrow {IA} ) + \dfrac{c}{{a + b + c}}(\overrightarrow {IC}  - \overrightarrow {IA} ).\end{array}\)

Suy ra

\(\left( {1 - \dfrac{{b + c}}{{a + b + c}}} \right)\overrightarrow {IA}  + \dfrac{b}{{a + b + c}}\overrightarrow {IB}  + \dfrac{c}{{a + b + c}}\overrightarrow {IC}  = \overrightarrow 0 \\ \Leftrightarrow \,\,\,a\overrightarrow {IA}  + b\overrightarrow {IB}  + c\overrightarrow {IC}  = \overrightarrow 0 .\)

Sachbaitap.com