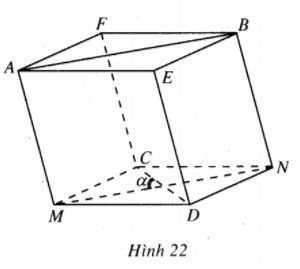
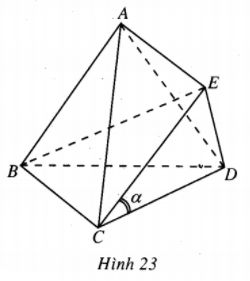
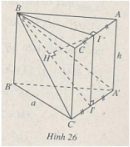
Bài 38 trang 10 Sách bài tập Hình học lớp 12 Nâng caoCho tứ diện ABCD. Cho tứ diện ABCD. Gọi d là khoảng cách giữa hai đường thẳng AB và CD, \(\alpha \) là góc giữa hai đường thẳng đó. Chứng minh rằng \({V_{ABCD}} = {1 \over 6}AB.CD.d.\sin \alpha .\) Giải Cách 1. Dựng hình hộp AEBF.MDNC ( gọi là hình hộp ngoại tiếp tứ diện ABCD) (h.22). Vì \(\left( {AEBF} \right)//\left( {MDNC} \right)\) nên chiều cao của hình hộp bằng khoảng cách d giữa AB và CD. Theo bài 37 ta có : \({V_{ABCD}} = {1 \over 3}\) Vhộp \(\eqalign{ & = {1 \over 3}{S_{MDNC}}.d \cr & = {1 \over 3}.{1 \over 2}MN.CD\sin \alpha .d = {1 \over 6}AB.CD.d\sin \alpha . \cr} \) Cách 2. (h.23) Dựng hình bình hành ABCE . Khi đó : \({V_{A.BCD}} = {V_{E.BCD}}\) (do \(AE//\left( {BCD} \right)\)) (1) \(\eqalign{ & {V_{E.BCD}} = {V_{B.ECD}}\;\;\;\;\;(2) \cr & {V_{B.ECD}} = {1 \over 3}{S_{ECD}}.d\left( {B,\left( {CDE} \right)} \right)\;\;\;(3) \cr & \cr} \) \({S_{ECD}} = {1 \over 2}CE.CD.\sin \widehat {ECD}\) \(\eqalign{ & = {1 \over 2}AB.CD\sin \alpha \;\;\;\;\;\;\;\;\;\;\;\;(4) \cr} \) \(d\left( {B,\left( {CDE} \right)} \right) = d\left( {AB,CD} \right)(\) do \(AB//\left( {CDE} \right))\;(5)\) Từ (1), (2), (3), (4), (5) suy ra : \({V_{ABCD}} = {1 \over 6}AB.CD.d\sin \alpha .\) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 4. Thể tích của khối đa diện
|
-
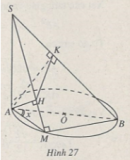
Bài 42 trang 11 Sách bài tập Hình học lớp 12 Nâng cao
Cho đường tròn đường kính AB nằm trên mặt phẳng

 Tải ngay
Tải ngay