Tải ngay
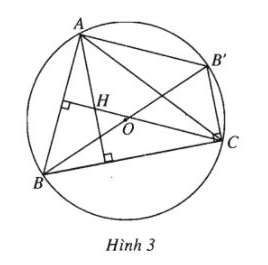
Bài 4 trang 5 SBT Hình học 10 Nâng caoGiải bài tập Bài 4 trang 5 SBT Hình học 10 Nâng cao Cho tam giác ABC nội tiếp trong đường tròn (O). Gọi H là trực tâm tam giác ABC và B’ là điểm đối xứng với B qua tâm O. Hãy so sánh các vec tơ \(\overrightarrow {AH} \) và \(\overrightarrow {B'C} \), \(\overrightarrow {AB'} \) và \(\overrightarrow {HC} \). Giải:
Chứng tỏ rằng AHCB’ là hình bình hành. Từ đó suy ra \(\overrightarrow {AH} \) = \(\overrightarrow {B'C} \), \(\overrightarrow {AB'} \) = \(\overrightarrow {HC} \). Sachbaitap.com
Xem thêm tại đây:
Bài 1, 2, 3. Vec tơ, tổng, hiệu của hai vec tơ
|
