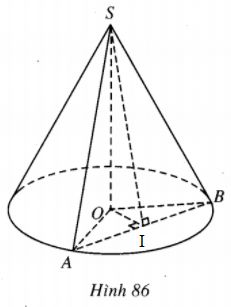
Bài 42 trang 62 Sách bài tập Hình học lớp 12 Nâng caoCho hình nón đỉnh S, đường cao SO. Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O dến AB bằng a và \(\widehat {SAO}\) = 300, \(\widehat {SAB}\) = 600. Tính diện tích xung quanh hình nón. Giải
Gọi \(I\) là trung điểm của AB thì \(OI \bot AB,SI \bot AB,OI = a.\) Ta có \(AO = SA\cos \) \(\widehat {SAO} ={{\sqrt 3 } \over 2}SA.\) \(AI = SA\cos \) \(\widehat {SAI} ={1 \over 2}SA.\) Từ đó \({{AI} \over {AO}} = {1 \over {\sqrt 3 }}.\) Mặt khác \({{AI} \over {AO}} = \cos \widehat {IAO}\) \( \Rightarrow \sin \widehat {IAO} ={{\sqrt 6 } \over 3} = {a \over {OA}}.\) Vậy \(OA = {{3a} \over {\sqrt 6 }} = {{a\sqrt 6 } \over 2}.\) Xét tam giác SAO, ta có \(SA = {{OA} \over {\cos {{30}^0}}} = {{a\sqrt 6 } \over 2}.{2 \over {\sqrt 3 }} = a\sqrt 2 .\) Từ đó diện tích xung quanh của hình nón đã cho là \({S_{xq}} = \pi .OA.SA = \pi .{{a\sqrt 6 } \over 2}.a\sqrt 2 = \pi {a^2}\sqrt 3 .\) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 4. Mặt nón, hình nón và khối nón
|
-
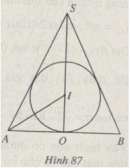
Bài 43 trang 62 Sách bài tập Hình học lớp 12 Nâng cao
Đường cao của hình nón gấp hai lần bán kính đáy của nó.
-
Bài 44 trang 63 Sách bài tập Hình học lớp 12 Nâng cao
Trong tất cả các hình nón nội tiếp hình cầu bán kính R

 Tải ngay
Tải ngay