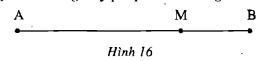Bài 45, 46, 47, 48, 49, 50, 51, 52, 53 trang 59, 60 SGK Toán 9 tập 2 - Luyện tập

Bài 45 trang 59 SGK Toán lớp 9 tập 2

Câu hỏi:

Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109. Tìm hai số đó.

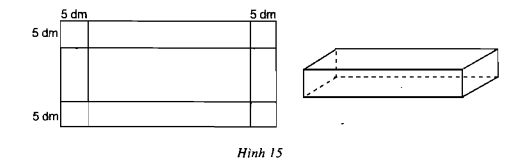
Bước 1: Lập phương trình

1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)

2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết 

3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.

Lời giải:

Gọi số bé là \(x\), \(x ∈ N, x > 0\), số tự nhiên liền sau của \(x\) là \(x + 1\).

Tích của hai số này là \(x(x + 1) = x^2+ x\)

Tổng của hai số này là: \(x+x + 1=2x+1\)

Theo đầu bài, tích của hai số lớn hơn tổng của chúng là 109 nên ta có phương trình:

\(x^2 + x - (2x + 1) = 109\) hay \(x^2- x - 110 = 0\)

Giải phương trình: \(\Delta = (-1) ^2 - 4. (-110) = 1 + 440 = 441\), \(\sqrt{\Delta} = 21\)

\({x_1}  = \dfrac{{ - \left( { - 1} \right) + 21}}{2}=11,\)\( {x_2} = \dfrac{{ - \left( { - 1} \right) - 21}}{2}= -10\)

Vì \(x > 0\) nên \({x_2} = -10\) không thỏa mãn điều kiện của ẩn. 

Do đó, số bé là 11 nên số liền sau nó là 11+1 = 12

Vậy hai số phải tìm là: 11 và 12. 

Bài 46 trang 59 SGK Toán lớp 9 tập 2

Câu hỏi:

Một mảnh đất hình chữ nhật có diện tích \(240\) m². Nếu tăng chiều rộng \(3\) m và giảm chiều dài \(4\) m thì diện tích mảnh đất không đổi. Tính kích thước của mảnh đất.

Phương pháp:

Các bước giải bài toán bằng cách lập phương trình

Bước 1: Lập phương trình

1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)

2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết 

3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.

Chú ý: Diện tích hình chữ nhật bằng tích chiều dài với chiều rộng.

Lời giải:

Gọi chiều rộng của mảnh đất là \(x\) (m), \(x > 0\).

Vì diện tích của mảnh đất bằng \(240\) m² nên chiều dài là: \(\dfrac{240}{x}\) (m)

Nếu tăng chiều rộng \(3\)m và giảm chiều dài \(4\)m thì mảnh đất mới có chiều rộng là \(x + 3\) (m), chiều dài là (\(\dfrac{240}{x}- 4)\) (m) và diện tích là: \((x + 3)(\dfrac{240}{x}-4)=240 - 4x + \dfrac{{720}}{x} - 12\) \((m^2) \)  

Theo đầu bài ta có phương trình:  

\(\begin{array}{l}
240 - 4x + \dfrac{{720}}{x} - 12 = 240\\
 \Rightarrow  - 4{x^2} + 720 - 12x = 0\\
 \Leftrightarrow {x^2} + 3x - 180 = 0
\end{array}\)

Giải phương trình: \(\Delta = 3^2 + 720 = 729\), \(\sqrt{\Delta} = 27\)

Suy ra \({x_1}  = \dfrac{{ - 3 + 27}}{2}= 12, \)\({x_2}  = \dfrac{{ - 3 - 27}}{2}= -15\)

Vì \(x > 0\) nên \({x_2} = -15\) không thỏa mãn điều kiện của ẩn. Do đó chiều rộng là \(12\)m, chiều dài là: \(240 : 12 = 20\) (m)

Vậy mảnh đất có chiều rộng là \(12\)m, chiều dài là \(20\)m.

Bài 47 trang 59 SGK Toán lớp 9 tập 2

Câu hỏi:

Bác Hiệp và cô Liên đi xe đạp từ làng lên tỉnh trên quãng đường dài \(30\) km, khởi hành cùng một lúc. Vận tốc xe của bác Hiệp lớn hơn vận tốc xe của cô Liên là \(3\) km/h nên bác Hiệp đã đến tỉnh sớm hơn cô Liên nửa giờ. Tính vận tốc xe mỗi người.

Phương pháp:

Các bước giải bài toán bằng cách lập phương trình

Bước 1: Lập phương trình

1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)

2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết 

3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.

Lời giải:

Gọi vận tốc của bác Hiệp là \(x\) (km/h),  khi đó vận tốc của cô Liên là \(x - 3\) (km/h), \(x > 3\).

Thời gian bác Hiệp đi từ làng lên tỉnh là \(\dfrac{30}{x}\) (giờ).

Thời gian cô Liên đi từ làng lên tỉnh là: \(\dfrac{30}{x-3}\) (giờ)

Vì bác Hiệp đến trước cô Liên nửa giờ, tức là thời gian đi của bác Hiệp ít hơn thời gian cô Liên nửa giờ nên ta có phương trình:

\(\dfrac{30}{x-3}-\dfrac{30}{x}\) = \(\dfrac{1}{2}\)

Giải phương trình:

\(\begin{array}{l}
30.2x - 30.2\left( {x - 3} \right) = x\left( {x - 3} \right)\\
 \Leftrightarrow 60x - 60x + 180 = {x^2} - 3x\\
 \Leftrightarrow {x^2} - 3x - 180 = 0\\
\Delta  = {\left( { - 3} \right)^2} - 4.1.\left( { - 180} \right) = 729 > 0,\sqrt \Delta   = 27
\end{array}\)

\({x_1}  = \dfrac{{3 + 27}}{2}= 15,\)\( {x_2} = \dfrac{{3 - 27}}{2}= -12\)

Vì \(x > 3 \) nên \({x_2} = -12\) không thỏa mãn điều kiện của ẩn.

Vậy vận tốc của bác Hiệp là 15 km/h

Vận tốc của cô Liên là 12 km/h 

Bài 48 trang 59 SGK Toán lớp 9 tập 2

Câu hỏi:

Từ một miếng tôn hình chữ nhật người ta cắt ở bốn góc bốn hình vuông có cạnh bằng \(5\) dm để làm thành một cái thùng hình hộp chữ nhật không nắp có dung tích \(1500\) dm³ (h.15). Hãy tính kích thước của miếng tôn lúc đầu, biết rằng chiều dài của nó gấp đôi chiều rộng.

Phương pháp:

Các bước giải bài toán bằng cách lập phương trình

Bước 1: Lập phương trình

1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)

2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết 

3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.

Chú ý: Thể tích hình hộp chữ nhật bằng tích của chiều dài, chiều rộng và chiều cao.

Lời giải:

Gọi chiều rộng của miếng tôn là \(x\) (dm), \(x > 10\).

Chiều dài của nó là \(2x\) (dm)

Khi làm thành một cái thùng hình hộp chữ nhật không nắp thì chiều dài của thùng là \(2x - 10\) (dm), chiều rộng là \(x - 10\) (dm), chiều cao là \(5\) (dm).

Dung tích của thùng là \(5(2x - 10)(x - 10)\) \((dm^3)\)

Theo đầu bài ta có phương trình:

\(\begin{array}{l}
5\left( {2x - 10} \right)\left( {x - 10} \right) = 1500\\
 \Leftrightarrow 5\left( {2{x^2} - 20x - 10x + 100} \right) = 1500\\
 \Leftrightarrow 2{x^2} - 30x + 100 = 300\\
 \Leftrightarrow {x^2} - 15x - 100 = 0
\end{array}\)

Giải phương trình: \(\Delta = 225 + 400 = 625 >0\), \(\sqrt{\Delta} = 25\)

Suy ra \({x_1} = 20, {x_2} = -5\) (loại) 

Vậy miếng tôn có chiều rộng bằng 20 (dm), chiều dài bằng 40 (dm).

Bài 49 trang 59 SGK Toán lớp 9 tập 2

Câu hỏi:

 Hai đội thợ quét sơn một ngôi nhà. Nếu họ cùng làm thì trong 4 ngày xong việc. Nếu họ làm riêng thì đội I hoàn thành công việc nhanh hơn đội II là 6 ngày. Hỏi nếu làm riêng thì mỗi đội phải làm trong bao nhiêu ngày để xong việc ?

Lời giải:

Gọi thời gian đội I làm một mình xong việc là \(x\) (ngày), \(x > 0\).

Vì đội II hoàn thành công việc lâu hơn đội I là 6 ngày nên thời gian một mình đội II làm xong việc là \(x + 6\) (ngày).

Mỗi ngày đội I làm được \(\dfrac{1}{x}\) (công việc).

Mỗi ngày đội II làm được \(\dfrac{1}{x+6}\) (công việc)

Hai đội làm 4 ngày xong công việc nên mỗi ngày cả hai đội làm được \(\dfrac{1}{4}\) công việc ta có phương trình:

\(\dfrac{1}{x}\) + \(\dfrac{1}{x+6}\) = \(\dfrac{1}{4}\)

\(\begin{array}{l}
 \Rightarrow 4\left( {x + 6} \right) + 4.x = x\left( {x + 6} \right)\\
 \Leftrightarrow 4x + 24 + 4x = {x^2} + 6x\\
 \Leftrightarrow {x^2} - 2x - 24 = 0
\end{array}\)

\(\Delta' = 1 + 24 = 25 = 5^2\)

\({x_1} = 1 + 5 = 6, {x_2} = 1 - 5 = -4\)

Vì \(x > 0\) nên \({x_2}  = -4\) không thỏa mãn điều kiện của ẩn.

Vậy một mình đội I làm trong \(6\) ngày thì xong việc.

Một mình đội II làm trong \(6 + 6 = 12\) ngày thì xong việc. 

Bài 50 trang 59 SGK Toán lớp 9 tập 2

Câu hỏi:

Miếng kim loại thứ nhất nặng \(880\) g, miếng kim loại thứ hai nặng \(858\) g. Thể tích của miếng thứ nhất nhỏ hơn thể tích của miếng thứ hai là \(10\) cm³, nhưng khối lượng riêng của miếng thứ nhất lớn hơn khối lượng riêng của miếng thứ hai là \(1\) g/cm³ . Tìm khối lượng riêng của mỗi miếng kim loại.

Bước 1: Lập phương trình

1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)

2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết 

3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.

Chú ý: Thể tích của 1 vật đồng nhất (về cấu tạo) với một hình dạng bất kỳ được tính theo công thức sau:

\(V = \dfrac{m}{D}\) 

Trong đó:

m là khối lượng của vật.

D là khối lượng riêng của chất tạo ra vật đó.

Lời giải:

Gọi khối lượng riêng của miếng kim loại thứ nhất là: \(x\) (g/cm³ ) 

Khối lượng riêng của miếng kim loại thứ hai là: \(x - 1\) (g/cm³ ) điều kiện \(x > 1\)

Thể tích của miếng kim loại thứ nhất là: \(\dfrac{880}{x}\)  (cm³ )

Thể tích của miếng kim loại thứ hai là: \(\dfrac{858}{x-1}\) (cm³ )

Theo đầu bài thể tích của miếng thứ nhất nhỏ hơn miếng thứ hai là \(10\) cm³ nên ta có phương trình: \(\dfrac{858}{x-1} - \dfrac{880}{x} = 10\)

\(\begin{array}{l}
 \Rightarrow 858x - 880\left( {x - 1} \right) = 10x\left( {x - 1} \right)\\
 \Leftrightarrow 858x - 880x + 880 = 10{x^2} - 10x\\
 \Leftrightarrow 10{x^2} + 12x - 880 = 0\\
 \Leftrightarrow 5{x^2} + 6x - 440 = 0 
\end{array}\)

Ta có: \(\Delta'=9 + 2200 = 2209\), \(\sqrt{\Delta' }= 47\)

Suy ra \({x_1} = \dfrac{{ - 3 + 47}}{5}= 8,8;\)\( {x_2}  = \dfrac{{ - 3 - 47}}{5}= -10\)

Vì \(x > 1\) nên \({x_2} = -10\) (loại) 

Vậy khối lượng riêng của miếng kim loại thứ nhất là: \(8,8\) g/cm³

Khối lượng riêng của miếng kim loại thứ hai là: \(7,8\) g/cm³

Bài 51 trang 59 SGK Toán lớp 9 tập 2

Câu hỏi:

 Người ta đổ thêm \(200\) g nước vào một dung dịch chứa \(40\) g muối thì nồng độ của dung dịch giảm đi \(10\) %. Hỏi trước khi đổ thêm nước thì dung dịch chứa bao nhiêu nước ?

Phương pháp: 

Các bước giải bài toán bằng cách lập phương trình

Bước 1: Lập phương trình

1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)

2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết 

3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.

Chú ý: Nồng độ dung dịch  

\(C = \dfrac{{{m_{ct}}}}{{{m_{dd}}}}\)  trong đó \({m_{ct}}\) là khối lượng chất tan, \({m_{dd}} = {m_{ct}} + {m_n}\) là khối lượng dung dịch bằng tổng khối lượng chất tan và khối lượng nước.

Lời giải:

Gọi khối lượng nước trong dung dịch trước khi đổ thêm nước là: \(x\) (g), \(x > 0\)

Nồng độ muối của dung dịch khi đó là: \(\dfrac{40}{x + 40}\)

Nếu đổ thêm \(200\) g nước vào dung dịch thì khối lượng của dung dịch sẽ là: \(x + 40 + 200\) (g)

Nồng độ của dung dịch bây giờ là: \(\dfrac{40}{x + 240}\)

Vì nồng độ muối giảm \(10\)% nên ta có phương trình:

\(\dfrac{40}{x + 40}-\dfrac{40}{x + 240}\) = \(10\)%

\(\begin{array}{l} \Leftrightarrow \dfrac{{40}}{{x + 40}} - \dfrac{{40}}{{x + 240}} = \dfrac{1}{{10}}\\ \Leftrightarrow \dfrac{{40.(x + 240)}}{{(x + 40).(x + 240)}} - \dfrac{{40.(x + 40)}}{{(x + 240).(x + 40)}} = \dfrac{1}{{10}}\\ \Leftrightarrow \dfrac{{40.(x + 240) - 40.(x + 40)}}{{(x + 40).(x + 240)}} = \dfrac{1}{{10}}\\ \Rightarrow 1.(x + 40).(x + 240) = 10.[40.(x + 240) - 40.(x + 40)]\end{array}\)

\(\Leftrightarrow (x + 40)(x + 240) = 400(x + 240 - x - 40)\)

hay \(x^2 + 280x - 70400 = 0\)

\(\Delta' = 19600 + 70400 = 90000\), \(\sqrt{\Delta'} = 300\)

\(\Rightarrow\) \({x_1} = 160, {x_2} = -440\)

Vì \(x > 0\) nên \({x_2} = -440\) (loại)

Vậy trước khi đổ thêm nước, trong dung dịch có \(160\) g nước.

Bài 52 trang 60 SGK Toán lớp 9 tập 2

Câu hỏi:

Khoảng cách giữa hai bên sông A và B là \(30\) km. Một canô đi từ bến A đến bến B, nghỉ \(40\) phút ở bến B rồi quay lại bến A. Kể từ lúc khởi hành đến khi về tới bến A hết tất cả \(6\) giờ. Hãy tìm vận tốc của canô trong nước yên lặng, biết rằng vận tốc của nước chảy là \(3\) km/h.

Phương pháp: 

Các bước giải bài toán bằng cách lập phương trình

Bước 1: Lập phương trình

1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)

2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết 

3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.

Chú ý: Đối với chuyển động của ca nô thì

\({v_{xd}} = {v_t} + {v_n};\,{v_{nd}} = {v_t} - {v_n}\)

Trong đó \({v_{xd}}\) là vận tốc ca nô khi xuôi dòng; \({v_{nd}}\) là vận tốc ca nô khi ngược dòng

\({v_t}\) là vận tốc thực của ca nô khi nước yên lặng; \({v_n}\) là vận tốc chảy của dòng nước

Lời giải:

Gọi vận tốc thực của canô (khi nước yên lặng) là \(x\) (km/h) , nên vận tốc khi đi xuôi dòng là: \(x + 3\) (km/h) và vận tốc khi ngược dòng là: \(x - 3\) (km/h), \(x > 3\).

Thời gian xuôi dòng là: \(\dfrac{30}{x + 3}\) (giờ)

Thời gian ngược dòng là: \(\dfrac{30}{x - 3}\) (giờ)

Nghỉ lại \(40\) phút hay \(\dfrac{2}{3}\) giờ ở B.

Theo đầu bài kể từ khi khời hành đến khi về tới bến A hết tất cả \(6\) giờ nên ta có phương trình: \(\dfrac{30}{x+ 3}+ \dfrac{30}{x- 3}+ \dfrac{2}{3} = 6\)

\(\begin{array}{l}
 \Leftrightarrow \dfrac{{30}}{{x + 3}} + \dfrac{{30}}{{x - 3}} = \dfrac{{16}}{3}\\
 \Rightarrow 30.3\left( {x - 3} \right) + 30.3.\left( {x + 3} \right) = 16.\left( {x - 3} \right)\left( {x + 3} \right)\\
 \Leftrightarrow 90x - 270 + 90x + 270 = 16\left( {{x^2} - 9} \right)\\
 \Leftrightarrow 16{x^2} - 180x - 144 = 0\\
 \Leftrightarrow 4{x^2} - 45x - 36 = 0
\end{array}\)

\(\Delta = 2025 + 576 = 2601 >0, \sqrt{\Delta} = 51\)

Suy ra \({x_1} = 12, {x_2} = -\dfrac{3}{4}\) (loại)

Vậy vận tốc của canô trong nước yên lặng là \(12\) km/h.

Bài 53 trang 60 SGK Toán lớp 9 tập 2

Câu hỏi:

Tỉ số vàng. Đố em chia được đoan AB cho trước thành hai đoạn sao cho tỉ số giữa đoạn lớn với đoạn AB bằng tỉ số giữa đoạn nhỏ với đoạn lớn (h.16).

Hãy tìm tỉ số ấy.

Đó chính là bài toán mà Ơ-clít đưa ra từ thế kỉ III trước công nguyên. Tỉ số nói trong bài toán được gọi là tỉ số vàng, còn phép chia nói trên được gọi là phép chia vàng hay phép chia hoàng kim.

Hướng dẫn: Giả sử M là điểm chia và AM > MB. Gọi tỉ số cần tìm là \(x\).

Lời giải:

Giả sử \(M\) là điểm chia đoạn \(AB\) sao cho \(AM>MB\) và \(AB\) có độ dài bằng \(a\).

Gọi độ dài của \(AM = x; 0 < x < a\). Khi đó \(MB = a - x\). 

Theo đầu bài: \(\displaystyle{{AM} \over {AB}} = {{MB} \over {AM}}\) hay \(\displaystyle {x \over a} = {{a - x} \over x}\)

Giải phương trình: \(x^2 = a(a - x)\) hay \(x^2 + ax - a^2= 0\)

\(\Delta = a^2 + 4a^2= 5a^2 , \sqrt{\Delta}= a\sqrt{5}\)

Suy ra \(\displaystyle {x_1} = {{ - a + a\sqrt 5 } \over 2} = {{a(\sqrt 5  - 1)} \over 2},{x_2} = {{ - a(\sqrt 5  + 1)} \over 2}\)

Vì \(x > 0\) nên \({x_2}\) không thỏa mãn điều kiện của ẩn.

Vậy \(\displaystyle AM={{a(\sqrt 5  - 1)} \over 2}\)

Tỉ số cần tìm là: \(\displaystyle {{AM} \over {AB}} = {{\sqrt 5  - 1} \over 2}\)

Sachbaitap.com